【题目】如图,一次函数y=kx+b的图象与反比例函数y=![]() 的图象相交于点A(-2,1),B(1,n).
的图象相交于点A(-2,1),B(1,n).
(1)求此一次函数和反比例函数的解析式;
(2)在平面直角坐标系的第二象限内边长为1的正方形EFDG的边均平行于坐标轴,若点E的坐标为(-a,a),当曲线y=![]() (x<0)与此正方形的边有交点时,求a的取值范围.
(x<0)与此正方形的边有交点时,求a的取值范围.

参考答案:
【答案】(1)反比例函数的解析式为y=-![]() ,一次函数的解析式为y=-x-1;(2)a的取值范围为
,一次函数的解析式为y=-x-1;(2)a的取值范围为![]() ≤a≤
≤a≤![]() +1.
+1.
【解析】(1)∵点A(﹣2,1)在反比例函数y=![]() 的图象上,
的图象上,
∴m=﹣2×1=﹣2,
∴反比例函数解析式为y=﹣![]() ;
;
∵点B(1,n)在反比例函数y=﹣![]() 的图象上,
的图象上,
∴﹣2=n,即点B的坐标为(1,﹣2).
将点A(﹣2,1)、点B(1,﹣2)代入y=kx+b中得:
![]() ,解得:
,解得:![]() ,
,
∴一次函数的解析式为y=﹣x﹣1 .
(2)不等式﹣x﹣1﹣(﹣![]() )<0可变形为:﹣x﹣1<﹣
)<0可变形为:﹣x﹣1<﹣![]() ,
,
观察两函数图象,发现:
当﹣2<x<0或x>1时,一次函数图象在反比例图象下方,
∴满足不等式kx+b﹣![]() <0的解集为﹣2<x<0或x>1.
<0的解集为﹣2<x<0或x>1.
(3)过点O、E作直线OE,如图所示.
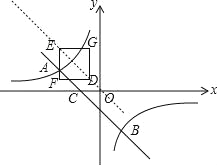
∵点E的坐标为(﹣a,a),
∴直线OE的解析式为y=﹣x.
∵四边形EFDG是边长为1的正方形,且各边均平行于坐标轴,
∴点D的坐标为(﹣a+1,a﹣1),
∵a﹣1=﹣(﹣a+1),
∴点D在直线OE上.
将y=﹣x代入y=﹣![]() (x<0)得:
(x<0)得:
﹣x=﹣![]() ,即x2=2,解得:x=﹣
,即x2=2,解得:x=﹣![]() ,或x=
,或x=![]() (舍去).
(舍去).
∵曲线y=﹣![]() (x<0)与此正方形的边有交点,
(x<0)与此正方形的边有交点,
∴﹣a≤﹣![]() ≤﹣a+1,解得:
≤﹣a+1,解得:![]() ≤a≤
≤a≤![]() +1.
+1.
故当曲线y=![]() (x<0)与此正方形的边有交点时,
(x<0)与此正方形的边有交点时,
a的取值范围为![]() ≤a≤
≤a≤![]() +1.
+1.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列各组数中,数值相等的是( )
A. ﹣22和(﹣2)2 B. 23和 32
C. ﹣33和(﹣3)3 D. (﹣3×2)2和﹣32×22
-
科目: 来源: 题型:
查看答案和解析>>【题目】一组数据10,13,9,16,13,10,13的众数与平均数的和是________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)解方程组: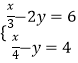
(2)求不等式﹣2<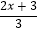 ≤2的整数解.
≤2的整数解. -
科目: 来源: 题型:
查看答案和解析>>【题目】某农场300名职工耕种51公顷土地,计划种植水稻、棉花和蔬菜,已知种植农作物每公顷所需的劳动力人数及投入的设备资金如下表:
农作物品种
每公顷需劳动力
每公顷需投入资金
水稻
4人
1万元
棉花
8人
1万元
蔬菜
5人
2万元
已知该农场计划在设备投入67万元,应该怎样安排这三种作物的种植面积,才能使所有职工有工作,而且投入的资金正好够用?
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列运动属于平移的是 ( )
A. 篮球运动员投出的篮球的运动 B. 空中放飞的风筝的运动
C. 乒乓球比赛中乒乓球的运动 D. 飞机在跑道上滑行到停止的运动
-
科目: 来源: 题型:
查看答案和解析>>【题目】一元二次方程x2+3=2x的根的情况为( )
A.有两个不相等的实数根
B.有两个相等的实数根
C.有一个实数根
D.没有实数根
相关试题

