【题目】如图,在平面直角坐标系xOy中,直线y=![]() x经过点A,作AB⊥x轴于点B,将△ABO绕点B逆时针旋转60°得到△CBD.若点B的坐标为(2,0),则点C的坐标为( )
x经过点A,作AB⊥x轴于点B,将△ABO绕点B逆时针旋转60°得到△CBD.若点B的坐标为(2,0),则点C的坐标为( )

A. (﹣1,![]() ) B. (﹣2,
) B. (﹣2,![]() ) C. (﹣
) C. (﹣![]() ,1) D. (﹣
,1) D. (﹣![]() ,2)
,2)
参考答案:
【答案】A
【解析】
过点C作CE⊥x轴于点E,在RT△AOB中,求出AO的长,根据旋转的性质可得AO=CD=4、OB=BD、△OBD是等边三角形,进而可得RT△COE中∠COE=60°、CO=2,由三角函数可得OE、CE.
过点C作CE⊥x轴于点E,

∵OB=2,AB⊥x轴,点A在直线y=![]() x上,
x上,
∴AB=2![]() ,OA=
,OA=![]() =4,
=4,
∴RT△ABO中,tan∠AOB=![]() =
=![]() ,
,
∴∠AOB=60°,
又∵△CBD是由△ABO绕点B逆时针旋转60°得到,
∴∠D=∠AOB=∠OBD=60°,AO=CD=4,
∴△OBD是等边三角形,
∴DO=OB=2,∠DOB=∠COE=60°,
∴CO=CDDO=2,
在RT△COE中,OE=COcos∠COE=2×![]() =1,
=1,
CE=COsin∠COE=2×![]() =
=![]() ,
,
∴点C的坐标为(1,![]() ),
),
故选:A.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知|a+b|+|a-b|-2b=0,在数轴上给出关于a,b的四种位置关系如图所示,则可能成立的有( )

A. 1种 B. 2种 C. 3种 D. 4种
-
科目: 来源: 题型:
查看答案和解析>>【题目】为确保信息安全,信息需要加密传输,其原理如下:

现将10个数字按图所示排成一个圈,并设置了一种数字信息的加密规则:加密钥匙为“n&3”,“n&3”代表“把明文n换成图中从它开始顺时针跳过3个数字的那个数字”,例如明文是5时,对应的密文为9.若收到的密文是6452,那么通过解密,它对应的明文是______.
-
科目: 来源: 题型:
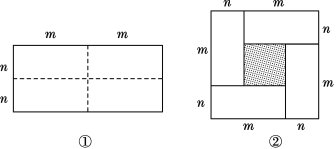
查看答案和解析>>【题目】图①是一个长为2m、宽为2n的长方形,沿图中虚线用剪刀把它均分成四个小长方形,然后按图②的形状拼成一个正方形.
(1)你认为图②中的阴影部分的正方形的边长等于多少?
(2)请用两种不同的方法求图②中阴影部分的面积.
(3)观察图②你能写出下列三个代数式之间的等量关系吗?
代数式:(m+n)2,(m-n)2,mn.
(4)根据(3)题中的等量关系,解决如下问题:
已知a+b=7,ab=5,求(a-b)2的值.(写出过程)
-
科目: 来源: 题型:
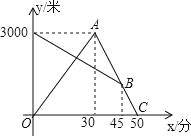
查看答案和解析>>【题目】某天早晨,张强从家跑步去体育锻炼,同时妈妈从体育场晨练结束回家,途中两人相遇,张强跑到体育场后发现要下雨,立即按原路返回,遇到妈妈后两人一起回到家(张强和妈妈始终在同一条笔直的公路上行走).如图是两人离家的距离y(米)与张强出发的时间x(分)之间的函数图象,根据图象信息解答下列问题:
(1)求张强返回时的速度;
(2)妈妈比按原速返回提前多少分钟到家?
(3)请直接写出张强与妈妈何时相距1000米?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC,AB=AC,以AB为直径的⊙O分别交AC、BC于点D、E,点F在AC的延长线上,且∠CBF=
 ∠CAB.
∠CAB. 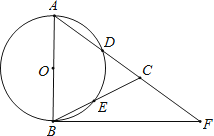
(1)求证:直线BF是⊙O的切线;
(2)若AB=5,sin∠CBF=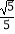 ,求BC和BF的长.
,求BC和BF的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,对称轴为直线x=
 的抛物线经过点A(6,0)和B(0,﹣4).
的抛物线经过点A(6,0)和B(0,﹣4). 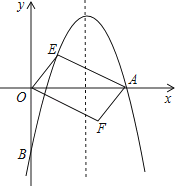
(1)求抛物线解析式及顶点坐标;
(2)设点E(x,y)是抛物线上一动点,且位于第一象限,四边形OEAF是以OA为对角线的平行四边形,求平行四边形OEAF的面积S与x之间的函数关系式;
(3)当(2)中的平行四边形OEAF的面积为24时,请判断平行四边形OEAF是否为菱形.
相关试题

