【题目】如图,对称轴为直线x= ![]() 的抛物线经过点A(6,0)和B(0,﹣4).
的抛物线经过点A(6,0)和B(0,﹣4). 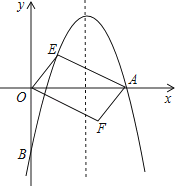
(1)求抛物线解析式及顶点坐标;
(2)设点E(x,y)是抛物线上一动点,且位于第一象限,四边形OEAF是以OA为对角线的平行四边形,求平行四边形OEAF的面积S与x之间的函数关系式;
(3)当(2)中的平行四边形OEAF的面积为24时,请判断平行四边形OEAF是否为菱形.
参考答案:
【答案】
(1)
解:设抛物线的解析式为y=ax2+bx+c,
将A、B点的坐标代入函数解析式,得
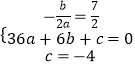 ,
,
解得 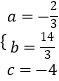 ,
,
抛物线的解析式为y=﹣ ![]() x2+
x2+ ![]() x﹣4,
x﹣4,
配方,得
y=﹣ ![]() (x﹣
(x﹣ ![]() )2+
)2+ ![]() ,
,
顶点坐标为( ![]() ,
, ![]() );
);
(2)
解:E点坐标为(x,﹣ ![]() x2+
x2+ ![]() x﹣4),
x﹣4),
S=2× ![]() OAyE=3(﹣
OAyE=3(﹣ ![]() x2+
x2+ ![]() x﹣4)
x﹣4)
即S=﹣2x2+14x﹣12;
(3)
解:平行四边形OEAF的面积为24时,平行四边形OEAF不能为菱形,理由如下:
当平行四边形OEAF的面积为24时,即
﹣2x2+14x﹣12=24,
化简,得
x2﹣7x+18=0,
△=b2﹣4ac=(﹣7)2﹣4×18=﹣23<0,
方程无解,
E点不存在,
平行四边形OEAF的面积为24时,平行四边形OEAF不能为菱形
【解析】(1)根据对称轴、A、B点的坐标,可得方程,根据解方程,可得答案;
(2)根据平行四边形的面积公式,可得函数解析式;
(3)根据函数值,可得E点坐标,根据菱形的判定,可得答案.本题考查了二次函数综合题,利用待定系数法求函数解析式,配方法求函数的顶点坐标;利用平行四边形性质是解题关键;利用方程的判别式是解题关键.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,直线y=
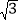 x经过点A,作AB⊥x轴于点B,将△ABO绕点B逆时针旋转60°得到△CBD.若点B的坐标为(2,0),则点C的坐标为( )
x经过点A,作AB⊥x轴于点B,将△ABO绕点B逆时针旋转60°得到△CBD.若点B的坐标为(2,0),则点C的坐标为( )
A. (﹣1,
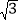 ) B. (﹣2,
) B. (﹣2,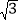 ) C. (﹣
) C. (﹣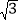 ,1) D. (﹣
,1) D. (﹣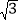 ,2)
,2) -
科目: 来源: 题型:
查看答案和解析>>【题目】某天早晨,张强从家跑步去体育锻炼,同时妈妈从体育场晨练结束回家,途中两人相遇,张强跑到体育场后发现要下雨,立即按原路返回,遇到妈妈后两人一起回到家(张强和妈妈始终在同一条笔直的公路上行走).如图是两人离家的距离y(米)与张强出发的时间x(分)之间的函数图象,根据图象信息解答下列问题:
(1)求张强返回时的速度;
(2)妈妈比按原速返回提前多少分钟到家?
(3)请直接写出张强与妈妈何时相距1000米?
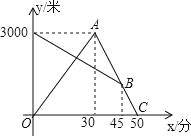
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC,AB=AC,以AB为直径的⊙O分别交AC、BC于点D、E,点F在AC的延长线上,且∠CBF=
 ∠CAB.
∠CAB. 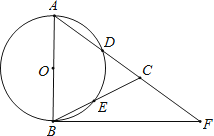
(1)求证:直线BF是⊙O的切线;
(2)若AB=5,sin∠CBF=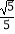 ,求BC和BF的长.
,求BC和BF的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图:已知正方形的边长为4,甲、乙两动点分别从正方形ABCD的顶点A、C同时沿正方形的边开始移动,甲点依顺时针方向环行,乙点依逆时针方向环行,若乙的速度是甲的速度的3倍,则它们第2018次相遇在边 ( )上.
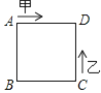
A. AB B. BC C. CD D. DA
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在菱形ABCD中,点F为对角线BD上一点,点E为AB的延长线上一点,DF=BE,CE=CF.求证:(1)△CFD≌△CEB;(2)∠CFE=60°.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=3,AC=4,BC=5,P为边BC上一动点,PE⊥AB于E,PF⊥AC于F,M为EF中点,则AM的最小值为_____.

相关试题

