【题目】已知正方形ABCD中,∠MAN=45°,∠MAN绕点A顺时针旋转,它的两边分别交CB、DC(或它们的延长线)于点M、N,当∠MAN绕点A旋转到BM=DN时(如图1),则
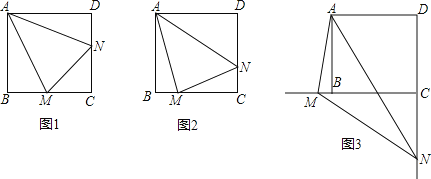
(1)线段BM、DN和MN之间的数量关系是______;
(2)当∠MAN绕点A旋转到BM≠DN时(如图2),线段BM、DN和MN之间有怎样的数量关系?写出猜想,并加以证明;
(3)当∠MAN绕点A旋转到(如图3)的位置时,线段BM、DN和MN之间又有怎样的数量关系?请直接写出你的猜想.
参考答案:
【答案】(1)BM+DN=MN;(2)BM+DN=MN,证明详见解析;(3)DN-BM=MN,证明详见解析.
【解析】
(1)连接AC,交MN于点G,则可知AC垂直平分MN,结合∠MAN=45°,可证明△ABM≌△AGM,可得到BM=MG,同理可得到NG=DN,可得出结论;
(2)在MB的延长线上,截取BE=DN,连接AE,则可证明△ABE≌△ADN,可得到AE=AN,进一步可证明△AEM≌△ANM,可得结论BM+DN=MN;
(3)在DC上截取DF=BM,连接AF,可先证明△ABM≌△ADF,进一步可证明△MAN≌△FAN,可得到MN=NF,从而可得到DN﹣BM=MN.
(1)如图1,连接AC,交MN于点G.
∵四边形ABCD为正方形,∴BC=CD,且BM=DN,∴CM=CN,且AC平分∠BCD,∴AC⊥MN,且MG=GN,∴AM=AN.
∵AG⊥MN,∴∠MAG=∠NAG.
∵∠BAC=∠MAN=45°,即∠BAM+∠GAM=∠GAM+∠GAN,∴∠BAM=∠GAN=∠GAM.
在△ABM和△AGM中,∵ ,∴△ABM≌△AGM(AAS),∴BM=MG,同理可得GN=DN,∴BM+DN=MG+GN=MN.
,∴△ABM≌△AGM(AAS),∴BM=MG,同理可得GN=DN,∴BM+DN=MG+GN=MN.
故答案为:BM+DN=MN;
(2)猜想:BM+DN=MN,证明如下:
如图2,在MB的延长线上,截取BE=DN,连接AE.
在△ABE和△ADN中,∵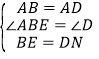 ,∴△ABE≌△ADN(SAS),∴AE=AN,∠EAB=∠NAD.
,∴△ABE≌△ADN(SAS),∴AE=AN,∠EAB=∠NAD.
∵∠BAD=90°,∠MAN=45°,∴∠BAM+∠DAN=45°,∴∠EAB+∠BAM=45°,∴∠EAM=∠NAM.
在△AEM和△ANM中,∵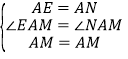 ,∴△AEM≌△ANM(SAS),∴ME=MN,又ME=BE+BM=BM+DN,∴BM+DN=MN;
,∴△AEM≌△ANM(SAS),∴ME=MN,又ME=BE+BM=BM+DN,∴BM+DN=MN;
(3)DN﹣BM=MN.证明如下:
如图3,在DC上截取DF=BM,连接AF.
△ABM和△ADF中,∵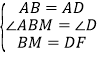 ,∴△ABM≌△ADF(SAS),∴AM=AF,∠BAM=∠DAF,∴∠BAM+∠BAF=∠BAF+∠DAF=90°,即∠MAF=∠BAD=90°.
,∴△ABM≌△ADF(SAS),∴AM=AF,∠BAM=∠DAF,∴∠BAM+∠BAF=∠BAF+∠DAF=90°,即∠MAF=∠BAD=90°.
∵∠MAN=45°,∴∠MAN=∠FAN=45°.
在△MAN和△FAN中,∵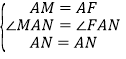 ,∴△MAN≌△FAN(SAS),∴MN=NF,∴MN=DN﹣DF=DN﹣BM,∴DN﹣BM=MN.
,∴△MAN≌△FAN(SAS),∴MN=NF,∴MN=DN﹣DF=DN﹣BM,∴DN﹣BM=MN.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知⊙O是等边三角形ABC的外接圆,点D在圆上,在CD的延长线上有一点F,使DF=DA,AE∥BC交CF于E.
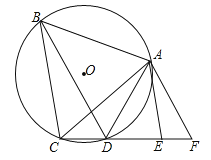
(1)求证:EA是⊙O的切线;
(2)求证:BD=CF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商品的进价为每件40元,售价为每件50元,每个月可卖出210件;如果每件商品的售价每上涨1元,则每个月少卖10件(每件售价不能高于65元),设每件商品的售价上涨
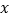 元(
元(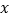 为正整数),每个月的销售利润为
为正整数),每个月的销售利润为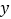 元.
元.(1)求
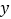 与
与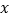 的函数关系式并直接写出自变量
的函数关系式并直接写出自变量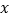 的取值范围;
的取值范围;(2)每件商品的售价定为多少元时,每个月可获得最大利润?最大月利润是多少元?
(3)每件商品的售价定为多少元时,每个月的利润恰为2 200元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市文化宫学习十九大有关优先发展教育的精神,举办了为某贫困山区小学捐赠书包活动.首次用2000元在商店购进一批学生书包,活动进行后发现书包数量不够,又购进第二批同样的书包,所购数量是第一批数量的3倍,但单价贵了4元,结果第二批用了6300元.
(1)求文化官第一批购进书包的单价是多少?
(2)商店两批书包每个的进价分别是68元和70元,这两批书包全部售给文化宫后,商店共盈利多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在△ABC中,AB=AC,点D是BC的中点,点E在AD上,连接BE、CE.
(1)求证:BE=CE
(2)如图2,若BE的延长线交AC于点F,且BF ⊥AC,垂足为F,原题设其它条件不变.求证:∠CAD=∠CBF
(3)在(2)的条件下,若∠BAC=45
 ,判断△CFE的形状,并说明理由.
,判断△CFE的形状,并说明理由.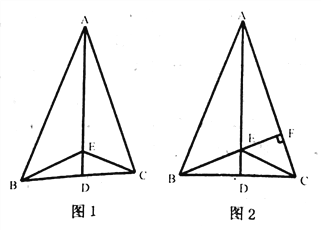
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
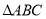 中,
中, ,
,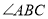 与
与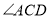 的平分线交于点
的平分线交于点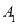 ,得
,得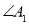 ;
;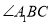 与
与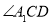 的平分线相交于点
的平分线相交于点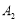 ,得
,得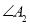 ;……;
;……;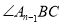 与
与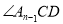 的平分线交于点
的平分线交于点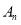 ,要使
,要使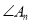 的度数为整数,则
的度数为整数,则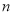 的最大值为( )
的最大值为( )
A.4B.5C.6D.7
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果抛物线y=-x2+bx+c经过A(0,-2),B(-1,1)两点,那么此抛物线经过
A. 第一、二、三、四象限 B. 第一、二、三象限
C. 第一、二、四象限 D. 第二、三、四象限
相关试题

