【题目】阅读材料:
关于三角函数还有如下的公式:
sin(α±β)=sin αcos β±cos αsin β
tan(α±β)= ![]()
利用这些公式可以将一些不是特殊角的三角函数转化为特殊角的三角函数来求值.
例:tan 15°=tan(45°-30°)=  =2-
=2-![]() .
.
根据以上阅读材料,请选择适当的公式解答下面问题:
(1)计算sin 15°的值.
(2)乌蒙铁塔是六盘水市标志性建筑物之一,小华想用所学的知识来测量该铁塔的高度.如图,小华站在离铁塔底A距离7 m的C处,测得铁塔顶B的仰角为75°,小华的眼睛离地面的距离DC为1.62 m,请帮助小华求出乌蒙铁塔的高度.(结果精确到0.1 m.参考数据: ![]() ≈1.732,
≈1.732, ![]() ≈1.414)
≈1.414)
![]()
参考答案:
【答案】(1)![]() ;(2)27.7m.
;(2)27.7m.
【解析】试题分析:(1)把15°化为45°-30°以后,再利用公式![]() 计算,即可求出
计算,即可求出![]() 的值;
的值;
(2)先根据锐角三角函数的定义求出![]() 的长,再根据
的长,再根据![]() 即可得出结论.
即可得出结论.
试题解析:(1)sin 15°=sin(45°-30°)=sin 45°cos 30°-cos 45°·sin 30°=![]() .
.
(2)在Rt△BDE中, ![]() tan∠BDE=
tan∠BDE=![]() ,
,
![]() BE=DE·tan∠BDE=7tan75°(m),
BE=DE·tan∠BDE=7tan75°(m),
![]() AB=AE+BE=1.62+7×
AB=AE+BE=1.62+7×![]() ,
,
=1.62+7×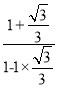 =1.62+7×
=1.62+7×![]() =1.62+7×(2+
=1.62+7×(2+![]() ),
),
≈1.62+7×(2+1.732),
=1.62+26.124=27.744≈27.7(m),
即乌蒙铁塔的高度约为27.7 m.
-
科目: 来源: 题型:
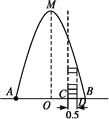
查看答案和解析>>【题目】如图,在水平地面点A处有一网球发射器向空中发射网球,网球飞行路线是一条抛物线,在地面上落点为B.有人在直线AB上点C处(靠点B一侧)竖直向上摆放无盖的圆柱形桶,试图让网球落入桶内.已知AB=4 m,AC=3 m,网球飞行最大高度OM=5 m,圆柱形桶的直径为0.5 m,高为0.3 m(网球的体积和圆柱形桶的厚度忽略不计).
(1)如果竖直摆放5个圆柱形桶时,网球能不能落入桶内?
(2)当竖直摆放圆柱形桶多少个时,网球可以落入桶内?
-
科目: 来源: 题型:
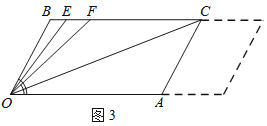
查看答案和解析>>【题目】已知:BC∥OA,∠B=∠A=120°,试回答下列问题:
(1)如图1所示,求证:OB∥AC;

(2)如图2,若点E、F在BC上,且满足∠FOC=∠AOC,并且OE平分∠BOF,则∠EOC的度数是______;

(3)在(2)的条件下,若平行移动AC,其它条件不变,如图3,则∠OCB:∠OFB的值是______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一次函数 y=kx+b(k≠0)的图象经过点(-1,-5),(2,1)两点.
(1)求 k 和 b 的值;
(2)一次函数 y=kx+b 图象与坐标轴所围成的三角形的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】由于“哈啰小蓝车”的投放使用,自行车正逐渐成为人们喜爱的交通工具.某商城的自行车销售量自 2019 年起逐月增加,据统计,该商城 9 月份销售自行车 64 辆,11 月份销售了 100 辆;
(1)若该商城 9 月至 11 月的自行车销售的月平均增长率相同,求自行车销售的月平均增长率.
(2)考虑到自行车需求不断增加,该商城准备再购进一批两种规格的自行车共 100 辆,已知 A 型车的进价为每辆 500 元,售价为每辆 700 元,B 型车的进价为每辆 1000 元,售价为每辆 1300 元.假设所购进车辆全部售完,为使利润不低于 26000 元,该商城购进 A 型车不超过多少辆?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,D、E、F是△ABC三边的中点,下列结论:①四边形AEDF,BDEF,CDFE都是平行四边形;②△ABC∽△DEF;③S△ABC=2S△DEF;④△DEF的周长是△ABC周长的一半,其中正确的序号是( )

A. ①②④ B. ①②③ C. ②③④ D. ①②③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于
 ,
, 的方程组
的方程组 ,则下列结论中:①当
,则下列结论中:①当 时,方程组的解是
时,方程组的解是 ;②当
;②当 ,
, 的值互为相反数时,
的值互为相反数时, ;③不存在一个实数
;③不存在一个实数 使得
使得 ;④若
;④若 ,则
,则 正确的个数有( )
正确的个数有( )A. 1个B. 2个C. 3个D. 4个
相关试题

