【题目】如图,直线y=﹣x+3与x轴、y轴分别交于点B、点C,经过B、C两点的抛物线y=x2+bx+c与x轴的另一个交点为A,顶点为P.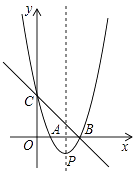
(1)求该抛物线的解析式;
(2)连接AC,在x轴上是否存在点Q,使以P、B、Q为顶点的三角形与△ABC相似?若存在,请求出点Q的坐标;若不存在,请说明理由.
参考答案:
【答案】
(1)
解:∵直线y=﹣x+3与x轴、y轴分别交于点B、点C,
令x=0,得y=3,
∴C(0,3),
令y=0,得x=3,
∴B(3,0),
∵经过B、C两点的抛物线y=x2+bx+c
∴ ![]() ,
,
解得 ![]() ,
,
∴抛物线解析式为y=x2﹣4x+3;
(2)
解:由(1),得A(1,0),连接BP,
∵∠CBA=∠ABP=45°,
∵抛物线解析式为y=x2﹣4x+3;
∴P(2,﹣1),
∵A(1,0),B(3,0),C(0,3),
∴BA=2,BC=3 ![]() ,BP=
,BP= ![]() ,
,
当△ABC∽△PBQ时,
∴ ![]() ,
,
∴ ![]() ,
,
∴BQ=3,
∴Q(0,0),
当△ABC∽△QBP时,
∴ ![]() ,
,
∴ ![]() ,
,
∴BQ= ![]() ,
,
∴Q( ![]() ,0),
,0),
∴Q点的坐标为(0,0)或( ![]() ,0).
,0).
【解析】(1)先确定出点B,C坐标,再用待定系数法求函数解析式;(2)先求出BA=2,BC=3 ![]() ,BP=
,BP= ![]() ,然后分两种情况①由△ABC∽△PBQ,得到
,然后分两种情况①由△ABC∽△PBQ,得到 ![]() ,求出BQ,②由△ABC∽△QBP得
,求出BQ,②由△ABC∽△QBP得 ![]() ,求出BQ,即可.
,求出BQ,即可.
【考点精析】本题主要考查了二次函数的图象的相关知识点,需要掌握二次函数图像关键点:1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】先化简,再求值
(1)(
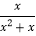 -1)
-1)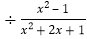 ,其中x的值从不等式
,其中x的值从不等式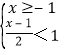 的正整数解中选取.
的正整数解中选取.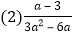 ÷(a+2-
÷(a+2-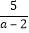 ),其中a2+3a-1=0.
),其中a2+3a-1=0. -
科目: 来源: 题型:
查看答案和解析>>【题目】某青春党支部在精准扶贫活动中,给结对帮扶的贫困家庭赠送甲、乙两种树苗让其栽种.已知乙种树苗的价格比甲种树苗贵10元,用480元购买乙种树苗的棵数恰好与用360元购买甲种树苗的棵数相同.
(1)求甲、乙两种树苗每棵的价格各是多少元?
(2)在实际帮扶中,他们决定再次购买甲、乙两种树苗共50棵,此时,甲种树苗的售价比第一次购买时降低了10%,乙种树苗的售价不变,如果再次购买两种树苗的总费用不超过1500元,那么他们最多可购买多少棵乙种树苗?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,BD为⊙O的直径,AB=AC,AD交BC于点E,AE=2,ED=4,

(1)求证:△ABE∽△ADB;
(2)求AB的长;
(3)延长DB到F,使得BF=BO,连接FA,试判断直线FA与⊙O的位置关系,并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】阅读理解:阅读下列材料:已知二次三项式2x2+x+a有一个因式是(x+2),求另一个因式以及a 的值
解:设另一个因式是(2x+b),
根据题意,得2x2+x+a=(x+2)(2x+b),
展开,得2x2+x+a =2x2+(b+4)x+2b,
所以
 ,解得
,解得 ,
,所以,另一个因式是(2x3),a 的值是6.
请你仿照以上做法解答下题:已知二次三项式3x2 10x m 有一个因式是(x+4),求另一个因式以及m的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】济南市某储运部紧急调拨一批物资,调进物资共用6小时,调进物资3小时后开始调出物资(调进物资与调出物资的速度均保持不变).储运部库存物资S(吨)与时间t(小时)之间的函数关系如图所示,这批物资从开始调进到全部调出需要的时间是( )

A. 6.2小时 B. 6.4小时 C. 6.6小时 D. 6.8小时
-
科目: 来源: 题型:
查看答案和解析>>【题目】温度与我们的生活息息相关,如图是一个温度计实物示意图,左边的刻度是摄氏温度(℃),右边的刻度是华氏温度(℉).设摄氏温度为x(℃)华氏温度为y(℉),则y是x的一次函数,通过观察我们发现,温度计上的摄氏温度为0℃时,华氏温度为32℉;摄氏温度为﹣20℃时,华氏温度为﹣4℉

请根据以上信息,解答下列问题
(1)仔细观察图中数据,试求出y与x的函数关系式;
(2)当摄氏温度为﹣5℃时,华氏温度为多少?
(3)当华氏温度为59℉时,摄氏温度为多少?
相关试题

