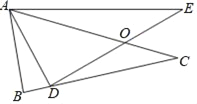
【题目】如图所示,已知△ABC中,D为BC上一点,E为△ABC外部一点,DE交AC于一点O,AC=AE,AD=AB,∠BAC=∠DAE.
(1)求证:△ABC≌△ADE;
(2)若∠BAD=20°,求∠CDE的度数.
参考答案:
【答案】(1)证明见解析;(2)∠CDE=20°.
【解析】试题分析:(1)根据题目中的条件,根据SAS可以证明结论成立;
(2)根据(1)中全等三角形的性质和三角形内角和的知识可以求得∠CDE的度数.
试题解析:(1)在△ABC和△ADE中,
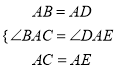 ,
,
∴△ABC≌△ADE(SAS);
(2)∵△ABC≌△ADE,
∴∠BAC=∠DAE,∠E=∠C,
∵∠BAC=∠BAD+∠DAC,∠DAE=∠DAC+∠CAE,∠BAD=20°,
∴∠CAE=∠BAD=20°,
∵∠E=∠C,∠AOE=∠DOC,
∴∠CAE=∠CDE,
∴∠CDE=20°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在正方形ABCD中,E为CD上一点,F为BC延长线上一点,且CE=CF.
(1)求证:△BCE≌△DCF;
(2)若∠FDC=30°,求∠BEF的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知线段AB=6cm,在直线AB上画线BC,使BC=11cm,则线段AC=( )
A.17cm
B.5cm
C.11cm或5cm
D.5cm或17cm -
科目: 来源: 题型:
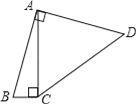
查看答案和解析>>【题目】如图,四边形ABCD中,∠BAD=∠ACB=90°,AB=AD,AC=4BC,设CD的长为x,四边形ABCD的面积为y,则y与x之间的函数关系式是( )
A. y=
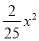 B. y=
B. y=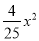 C. y=
C. y=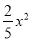 D. y=
D. y=
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在Rt△ABC中,∠C=90°,∠BAC的角平分线AD交BC边于D.
(1)以AB边上一点O为圆心,过A、D两点作⊙O(不写作法,保留作图痕迹),再判断直线BC与⊙O的位置关系,并说明理由;
(2)若(1)中的⊙O与AB边的另一个交点为E,AB=6,BD=2
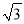 ,求线段BD、BE与劣弧DE所围成的图形面积.(结果保留根号和π)
,求线段BD、BE与劣弧DE所围成的图形面积.(结果保留根号和π)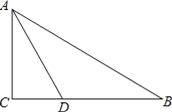
-
科目: 来源: 题型:
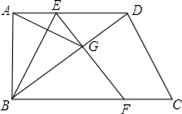
查看答案和解析>>【题目】如图,在梯形ABCD中,∠ABC=∠BAC=90°,在AD上取一点E,将△ABE沿直线BE折叠,使点A落在BD上的G处,EG的延长线交直线BC于点F.
(1)试探究AE、ED、DG之间有何数量关系?说明理由;
(2)判断△ABG与△BFE是否相似,并对结论给予证明;
(3)设AD=a,AB=b,BC=c.
①当四边形EFCD为平行四边形时,求a、b、c应满足的关系;
②在①的条件下,当b=2时,a的值是唯一的,求∠C的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】等边△ABC中,AO是BC边上的高,D为AO上一点,以CD为一边,在CD下方作等边△CDE,连接BE.

(1)求证:△ACD≌△BCE
(2)过点C作CH⊥BE,交BE的延长线于H,若BC=8,求CH的长.
相关试题

