【题目】在正方形ABCD中,E为CD上一点,F为BC延长线上一点,且CE=CF.
(1)求证:△BCE≌△DCF;
(2)若∠FDC=30°,求∠BEF的度数.

参考答案:
【答案】见解析
【解析】试题分析:
(1) 结合条件观察图形可知,在待求证的这组全等三角形中,有一组对应角∠BCE与∠DCF互补,根据四边形ABCD是正方形的条件易知∠BCE=∠DCF. 以这组对应角为着眼点进一步观察图形易知,作为正方形ABCD边的BC与DC相等,条件中又已知CE=CF,故可以利用SAS证明这组三角形全等.
(2) 求∠BEF的度数就是求∠BEC+∠CEF的度数. 在Rt△DCF中易知∠DFC的度数. 利用第(1)小题的结论可知∠BEC=∠DFC,从而得到∠BEC的度数. 利用条件可以得出△ECF为等腰直角三角形的结论,从而得到∠CEF的度数. 综合上面的结果即得∠BEF的度数.
试题解析:
(1) 证明:∵四边形ABCD是正方形,
∴BC=DC,∠BCD=90°,
∴∠DCF=∠BCD=90°,即∠BCE=∠DCF=90°,
∵在△BCE与△DCF中:
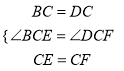 ,
,
∴△BCE≌△DCF (SAS).
(2) ∠BEF的度数为105°. 求解过程如下.
∵∠FDC=30°,∠DCF=90°,
∴在Rt△DCF中,∠DFC=90°-∠FDC=90°-30°=60°,
∵△BCE≌△DCF,
∴∠BEC=∠DFC=60°,
∵CE=CF,∠DCF=90°,
∴△ECF为等腰直角三角形,
∴∠CEF=∠CFE=45°,
∵∠BEC=60°,∠CEF=45°,
∴∠BEF=∠BEC+∠CEF=60°+45°=105°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】把一根木条钉在墙上,至少要钉_____个钉子,根据_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若3080000=3.08×10x,则x=_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算正确的是( )
A. a4a2=a8 B. a5+a5=a10
C. (﹣3a3)2=6a6 D. (a3)2a=a7
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知线段AB=6cm,在直线AB上画线BC,使BC=11cm,则线段AC=( )
A.17cm
B.5cm
C.11cm或5cm
D.5cm或17cm -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD中,∠BAD=∠ACB=90°,AB=AD,AC=4BC,设CD的长为x,四边形ABCD的面积为y,则y与x之间的函数关系式是( )
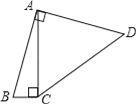
A. y=
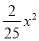 B. y=
B. y=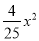 C. y=
C. y=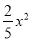 D. y=
D. y=
-
科目: 来源: 题型:
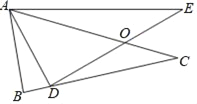
查看答案和解析>>【题目】如图所示,已知△ABC中,D为BC上一点,E为△ABC外部一点,DE交AC于一点O,AC=AE,AD=AB,∠BAC=∠DAE.
(1)求证:△ABC≌△ADE;
(2)若∠BAD=20°,求∠CDE的度数.
相关试题

