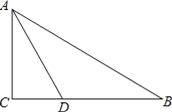
【题目】已知:如图,在Rt△ABC中,∠C=90°,∠BAC的角平分线AD交BC边于D.
(1)以AB边上一点O为圆心,过A、D两点作⊙O(不写作法,保留作图痕迹),再判断直线BC与⊙O的位置关系,并说明理由;
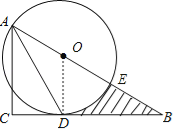
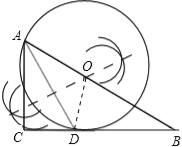
(2)若(1)中的⊙O与AB边的另一个交点为E,AB=6,BD=2![]() ,求线段BD、BE与劣弧DE所围成的图形面积.(结果保留根号和π)
,求线段BD、BE与劣弧DE所围成的图形面积.(结果保留根号和π)
参考答案:
【答案】(1)作图见解析;直线BC与⊙O的位置关系为相切,理由见解析;(2)线段BD、BE与劣弧DE所围成的图形面积为2![]() ﹣
﹣![]() π.
π.
【解析】试题分析:(1)根据题意得:O点应该是AD垂直平分线与AB的交点;由∠BAC的角平分线AD交BC边于D,与圆的性质可证得AC∥OD,又由∠C=90°,则问题得证;
(2)设⊙O的半径为r.则在Rt△OBD中,利用勾股定理列出关于r的方程,通过解方程即可求得r的值;然后根据扇形面积公式和三角形面积的计算可以求得“线段BD、BE与劣弧DE所围成的图形面积为:S△ODB﹣S扇形ODE=2![]() ﹣
﹣![]() π”.
π”.
解:(1)如图:连接OD,
∵OA=OD,
∴∠OAD=∠ADO,
∵∠BAC的角平分线AD交BC边于D,
∴∠CAD=∠OAD,
∴∠CAD=∠ADO,
∴AC∥OD,
∵∠C=90°,
∴∠ODB=90°,
∴OD⊥BC,
即直线BC与⊙O的切线,
∴直线BC与⊙O的位置关系为相切;
(2)设⊙O的半径为r,则OB=6﹣r,又BD=2![]() ,
,
在Rt△OBD中,
OD2+BD2=OB2,
即r2+(2![]() )2=(6﹣r)2,
)2=(6﹣r)2,
解得r=2,OB=6﹣r=4,
∴∠DOB=60°,
∴S扇形ODE=![]() =
=![]() π,
π,
S△ODB=![]() OD×BD=
OD×BD=![]() ×2×2
×2×2![]() =2
=2![]() ,
,
∴线段BD、BE与劣弧DE所围成的图形面积为:S△ODB﹣S扇形ODE=2![]() ﹣
﹣![]() π.
π.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知线段AB=6cm,在直线AB上画线BC,使BC=11cm,则线段AC=( )
A.17cm
B.5cm
C.11cm或5cm
D.5cm或17cm -
科目: 来源: 题型:
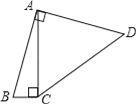
查看答案和解析>>【题目】如图,四边形ABCD中,∠BAD=∠ACB=90°,AB=AD,AC=4BC,设CD的长为x,四边形ABCD的面积为y,则y与x之间的函数关系式是( )
A. y=
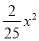 B. y=
B. y=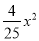 C. y=
C. y=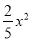 D. y=
D. y=
-
科目: 来源: 题型:
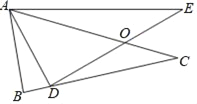
查看答案和解析>>【题目】如图所示,已知△ABC中,D为BC上一点,E为△ABC外部一点,DE交AC于一点O,AC=AE,AD=AB,∠BAC=∠DAE.
(1)求证:△ABC≌△ADE;
(2)若∠BAD=20°,求∠CDE的度数.
-
科目: 来源: 题型:
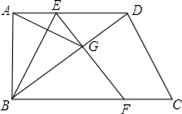
查看答案和解析>>【题目】如图,在梯形ABCD中,∠ABC=∠BAC=90°,在AD上取一点E,将△ABE沿直线BE折叠,使点A落在BD上的G处,EG的延长线交直线BC于点F.
(1)试探究AE、ED、DG之间有何数量关系?说明理由;
(2)判断△ABG与△BFE是否相似,并对结论给予证明;
(3)设AD=a,AB=b,BC=c.
①当四边形EFCD为平行四边形时,求a、b、c应满足的关系;
②在①的条件下,当b=2时,a的值是唯一的,求∠C的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】等边△ABC中,AO是BC边上的高,D为AO上一点,以CD为一边,在CD下方作等边△CDE,连接BE.

(1)求证:△ACD≌△BCE
(2)过点C作CH⊥BE,交BE的延长线于H,若BC=8,求CH的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知y=ax5+bx3+cx+14.当x=n时,y=20,则当x=﹣n时,y的值为_____.
相关试题

