【题目】如图,在正方形ABCD中,点E是AD的中点,连接BE、CE,点F是CE的中点,连接DF、
BF,点M是BF上一点且![]() =
=![]() ,过点M作MN⊥BC于点N,连接FN,则
,过点M作MN⊥BC于点N,连接FN,则![]() = .
= .

参考答案:
【答案】![]()
【解析】
试题分析:根据正方形的性质得到∠A=∠ABC=∠BCD=∠CDA=90°,AB=BC=CD=DA,AD∥BC.设AE=a,则DE=a,AB=BC=CD=DA=2a.根据勾股定理得到BE=![]() a,CE=
a,CE=![]() a,得到BE=CE,过点F作FG⊥AD于G,FG交BC于H.根据FG∥CD,点F是CE的中点,得到EG=DG=
a,得到BE=CE,过点F作FG⊥AD于G,FG交BC于H.根据FG∥CD,点F是CE的中点,得到EG=DG=![]() DE=
DE=![]() a,GF=
a,GF=![]() CD=a.根据三角函数的定义得到∠AEB=∠GDF,由平行线的性质得到∠BEF=∠DFE,推出△EFG≌△CFH,根据全等三角形的性质得到FG=FH=a,EG=CH=
CD=a.根据三角函数的定义得到∠AEB=∠GDF,由平行线的性质得到∠BEF=∠DFE,推出△EFG≌△CFH,根据全等三角形的性质得到FG=FH=a,EG=CH=![]() a.推出四边形CDGH是矩形,根据矩形的性质得到CH=DG=
a.推出四边形CDGH是矩形,根据矩形的性质得到CH=DG=![]() a,根据平行线分线段成比例定理得到
a,根据平行线分线段成比例定理得到![]() =
=![]() =
=![]() ,于是得到MN=
,于是得到MN=![]() FH=
FH=![]() a,BN=
a,BN=![]() BH=
BH=![]() a,求得S△FMN=
a,求得S△FMN=![]() =
=![]()
![]() a×a=
a×a=![]() a2,S四边形FEBN=S正方形ABCD﹣S△ABE﹣S△CDE﹣S△CNF=4a2﹣
a2,S四边形FEBN=S正方形ABCD﹣S△ABE﹣S△CDE﹣S△CNF=4a2﹣![]() 2aa﹣
2aa﹣![]() ﹣
﹣![]() =
=![]() a2.即可得到结论.
a2.即可得到结论.
解:∵四边形ABCD是正方形,
∴∠A=∠ABC=∠BCD=∠CDA=90°,AB=BC=CD=DA,AD∥BC.
设AE=a,则DE=a,AB=BC=CD=DA=2a.
在△ABE中,由勾股定理,得BE=![]() a,
a,
在△CDE中,由勾股定理,得CE=![]() a,
a,
∴BE=CE,
过点F作FG⊥AD于G,FG交BC于H.
∵AD∥BC,FG⊥AD,∴GH⊥BC.
∵FG∥CD,点F是CE的中点,
∴EG=DG=![]() DE=
DE=![]() a,GF=
a,GF=![]() CD=a.
CD=a.
在直角△ABE中,∵tan∠AEB=![]() =
=![]() =2,
=2,
在直角△GFD中,∵tan∠GDF=![]() =
=![]() =2,
=2,
∴tan∠AEB=tan∠GDF,
∵0°<∠AEB<90°,0°<∠GDF<90°,
∴∠AEB=∠GDF,
∴BE∥DF,
∴∠BEF=∠DFE,
在△EFG与△CFH中, ,
,
∴△EFG≌△CFH,
∴FG=FH=a,EG=CH=![]() a.
a.
∵GH∥CD,GD∥HC,∠CDA=90°,
∴四边形CDGH是矩形,
∴CH=DG=![]() a,
a,
∴BH=BC﹣CH=![]() a.
a.
∵MN⊥BC,GH⊥BC,
∴MN∥FH,
∴![]() =
=![]() =
=![]() ,
,
∴MN=![]() FH=
FH=![]() a,BN=
a,BN=![]() BH=
BH=![]() a,
a,
∴MN=![]() AB,
AB,
∵BN=CH=![]() a,
a,
∴NH=BC﹣BN﹣CH=a,
∴S△FMN=![]() =
=![]()
![]() a×a=
a×a=![]() a2,
a2,
S四边形FEBN=S正方形ABCD﹣S△ABE﹣S△CDE﹣S△CNF=4a2﹣![]() 2aa﹣
2aa﹣![]() ﹣
﹣![]() =
=![]() a2.
a2.
∴![]() =
=![]()
![]() =
=![]() .
.
故答案为:![]() .
.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图(1)四边形ABCD中,已知∠ABC+∠ADC=180°,AB=AD,DA⊥AB,点E在CD的延长线上,∠BAC=∠DAE.

(1)试说明:△ABC≌△ADE;
(2)试说明CA平分∠BCD;
(3)如图(2),过点A作AM⊥CE,垂足为M,试说明:∠ACE=∠CAM=∠MAE=∠E=45°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】有七张正面分别标有数字﹣2,﹣1,0,1,2,3,4的卡片,它们除数字不同外其余全部相同,现将它们背面朝上,洗匀后从中随机抽取一张,记卡片上的数字为a,则使关于x的一元二次方程x2﹣2(a﹣1)x+a2﹣3a=0有实数根,且
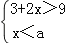 无解的概率是 .
无解的概率是 . -
科目: 来源: 题型:
查看答案和解析>>【题目】已知,如图,O为坐标原点,四边形OABC为矩形,A(10,0),C(0,4),点D是OA的中点,点P在边BC上以每秒1个单位长的速度由点C向点B运动.

(1)当t为何值时,四边形PODB是平行四边形?
(2)在线段PB上是否存在一点Q,使得ODQP为菱形?若存在,求t的值;若不存在,请说明理由;
(3)△OPD为等腰三角形时,写出点P的坐标(不必写过程).
-
科目: 来源: 题型:
查看答案和解析>>【题目】(12分)(2015秋万州区期末)在△ABC中,AB=AC,BG⊥AC于G,DE⊥AB于E,DF⊥AC于F.
(1)如图1,若D是BC边上的中点,∠A=45°,DF=3,求AC的长;
(2)如图2,D是线段BC上的任意一点,求证:BG=DE+DF;
(3)在图3,D是线段BC延长线上的点,猜想DE、DF与BG的关系,并证明.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD是菱形,对角线AC、BD相交于点O,DH⊥AB于H,连接OH,求证:∠DHO=∠DCO.

-
科目: 来源: 题型:
查看答案和解析>>【题目】将平行四边形纸片ABCD按如图方式折叠,使点C与点A重合,点D落到D’处,折痕为EF.
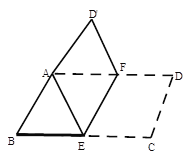
(1)、求证:△ABE≌△AD’F;
(2)、连接CF,判断四边形AECF是否为平行四边形?请证明你的结论。
(3)、若AE=5,求四边形AECF的周长。
相关试题

