【题目】如图,在平面直角坐标系中,O为坐标原点,直线y=﹣x﹣3与x轴交于点A,与y轴交于点C,抛物线y=x2+bx+c经过A、C两点,与x轴交于另一点B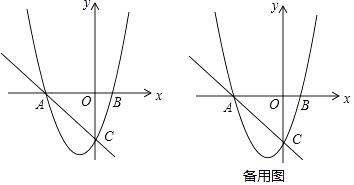
(1)求抛物线的解析式;
(2)点D是第二象限抛物线上的一个动点,连接AD、BD、CD,当S△ACD= ![]() S四边形ACBD时,求D点坐标;
S四边形ACBD时,求D点坐标;
(3)在(2)的条件下,连接BC,过点D作DE⊥BC,交CB的延长线于点E,点P是第三象限抛物线上的一个动点,点P关于点B的对称点为点Q,连接QE,延长QE与抛物线在A、D之间的部分交于一点F,当∠DEF+∠BPC=∠DBE时,求EF的长.
参考答案:
【答案】
(1)
解:∵令x=0得:y=﹣3,
∴C(0,﹣3).
令y=0得:﹣x﹣3=0,解得x=﹣3,
∴A(﹣3,0).
将A、C两点的坐标代入抛物线的解析式的: ![]() ,解得:
,解得: ![]() .
.
∴抛物线的解析式为y=x2+2x﹣3
(2)
解:如图1所示:
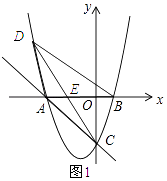
令y=0得:x2+2x﹣3=0,解得x=﹣3或x=1.
∴AB=4.
∵S△ACD= ![]() S四边形ACBD,
S四边形ACBD,
∴S△ADC:S△DCB=3:5.
∴AE:EB=3:5.
∴AE=4× ![]() =
= ![]() .
.
∴点E的坐标为(﹣ ![]() ,0).
,0).
设EC的解析式为y=kx+b,将点C和点E的坐标代入得: 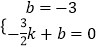 ,
,
解得:k=﹣2,b=﹣3.
∴直线CE的解析式为y=﹣2x﹣3.
将y=﹣2x﹣3与y=x2+2x﹣3联立,解得:x=﹣4或x=0(舍去),
将x=﹣4代入y=﹣2x﹣3得:y=5.
∴点D的坐标为(﹣4,5)
(3)
解:如图2所示:过点D作DN⊥x轴,垂足为N,过点P作PM⊥x轴,垂足为M.
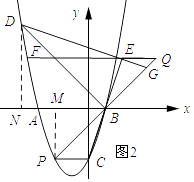
设直线BC的解析式为y=kx+b,将点C和点B的坐标代入得: ![]() ,
,
解得:k=3,b=﹣3.
∴直线BC的解析式为y=3x﹣3.
设直线DE的解析式为y=﹣ ![]() x+n,将点D的坐标代入得:﹣
x+n,将点D的坐标代入得:﹣ ![]() ×(﹣4)+n=5,解得n=5﹣
×(﹣4)+n=5,解得n=5﹣ ![]() =
= ![]() .
.
∴直线DE的解析式为y=﹣ ![]() x+
x+ ![]() .
.
将y=3x﹣3与y=﹣ ![]() x+
x+ ![]() 联立解得:x=2,y=3.
联立解得:x=2,y=3.
∴点E坐标为(2,3).
依据两点间的距离公式可知:BC=CE= ![]() .
.
∵点P与点Q关于点B对称,
∴PB=BQ.
在△PCB和△QEB中 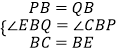 ,
,
∴△PCB≌△QEB.
∴∠BPC=∠Q.
又∵∠DEF+∠BPC=∠DBE,∠DEF=∠QEG,∠EGB=∠Q+∠QEG
∴∠DBE=∠DGB.
又∵∠DBE+∠BDE=90°,
∴∠DGB+∠BDG=90°,即∠PBD=90°.
∵D(﹣4,5),B(1,0),
∴DM=NB.
∴∠DBN=45°.
∴∠PBM=45°.
∴PM=MB
设点P的坐标为(a,a2+2a﹣3),则BM=1﹣a,PM=﹣a2﹣2a+3.
∴1﹣a=﹣a2﹣2a+3,解得:a=﹣2或a=1(舍去).
∴点P的坐标为(﹣2,3).
∴PC∥x轴.
∵∠Q=∠BPC,
∴EQ∥PC.
∴点E与点F的纵坐标相同.
将y=3代入抛物线的解析式得:x2+2x﹣3=3,解得:x=﹣1﹣ ![]() 或x=﹣1+
或x=﹣1+ ![]() (舍去).
(舍去).
∴点F的坐标为(﹣1 ![]() ,3).
,3).
∴EF=2﹣(﹣1﹣ ![]() )=3+
)=3+ ![]()
【解析】(1)先求得A、C两点的坐标,然后利用待定系数法求解即可;(2)先求得AB的长,然后依据S△ACD= ![]() S四边形ACBD , 求得AE的长,可得到E的坐标为(﹣
S四边形ACBD , 求得AE的长,可得到E的坐标为(﹣ ![]() ,0),利用待定系数法可求得CE的解析式,然后CE的解析式与抛物线的解析式联立可求得点D的坐标;(3)过点D作DN⊥x轴,垂足为N,过点P作PM⊥x轴,垂足为M.先求得BC和DE的解析式,从而可求得点E的坐标,然后可证明BC=BE,然后可证明△PCB≌△QEB,得到∠BPC=∠Q,依据题意可得到∠DBE=∠DGB.接下来,在证明∠PBD=90°,∠DBN=45°,然后可求得∠PBM=45°,设点P的坐标为(a,a2+2a﹣3),则BM=1﹣a,PM=﹣a2﹣2a+3然后依据PM=MB可求得a的值,则可得到点P的坐标,然后可证明EF∥x轴,最后将点F的纵坐标代入抛物线的解析式可求得点F的横坐标,最后依据EF=xE﹣xF求解即可.
,0),利用待定系数法可求得CE的解析式,然后CE的解析式与抛物线的解析式联立可求得点D的坐标;(3)过点D作DN⊥x轴,垂足为N,过点P作PM⊥x轴,垂足为M.先求得BC和DE的解析式,从而可求得点E的坐标,然后可证明BC=BE,然后可证明△PCB≌△QEB,得到∠BPC=∠Q,依据题意可得到∠DBE=∠DGB.接下来,在证明∠PBD=90°,∠DBN=45°,然后可求得∠PBM=45°,设点P的坐标为(a,a2+2a﹣3),则BM=1﹣a,PM=﹣a2﹣2a+3然后依据PM=MB可求得a的值,则可得到点P的坐标,然后可证明EF∥x轴,最后将点F的纵坐标代入抛物线的解析式可求得点F的横坐标,最后依据EF=xE﹣xF求解即可.
-
科目: 来源: 题型:
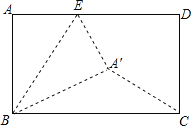
查看答案和解析>>【题目】如图,长方形ABCD中,∠A=∠ABC=∠BCD=∠D=90°,AB=CD=6,AD=BC=10,点E为射线AD上的一个动点,若△ABE与△A′BE关于直线BE对称,当△A′BC为直角三角形时,AE的长为______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为解决中小学大班额问题,东营市各县区今年将改扩建部分中小学,某县计划对A、B两类学校进行改扩建,根据预算,改扩建2所A类学校和3所B类学校共需资金7800万元,改扩建3所A类学校和1所B类学校共需资金5400万元.
(1)改扩建1所A类学校和1所B类学校所需资金分别是多少万元?
(2)该县计划改扩建A、B两类学校共10所,改扩建资金由国家财政和地方财政共同承担.若国家财政拨付资金不超过11800万元;地方财政投入资金不少于4000万元,其中地方财政投入到A、B两类学校的改扩建资金分别为每所300万元和500万元.请问共有哪几种改扩建方案?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,△ABC,△ADE均为等腰直角三角形,点D,E,C在同一直线上,连接BD.
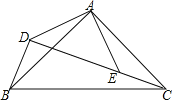
(1)求证:△ADB≌△AEC;
(2)若AD=AE=
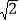 ,CE=2,求BC的长.
,CE=2,求BC的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】把几个图形拼成一个新的图形,再通过图形面积的计算,常常可以得到一些有用的式子,或可以求出一些不规则图形的面积.

(1)如图1,是将几个面积不等的小正方形与小长方形拼成一个边长为a+b+c的正方形,试用不同的方法计算这个图形的面积,你能发现什么结论,请写出来.
(2)如图2,是将两个边长分别为a和b的正方形拼在一起,B、C、G三点在同一直线上,连接BD和BF,若两正方形的边长满足a+b=10,ab=20,你能求出阴影部分的面积吗?
-
科目: 来源: 题型:
查看答案和解析>>【题目】一次数学活动中,检验两条纸带①、②的边线是否平行,小明和小丽采用两种不同的方法:小明对纸带①沿AB折叠,量得∠1=∠2=50°;小丽对纸带②沿GH折叠,发现GD与GC重合,HF与HE重合. 则下列判断正确的是( )
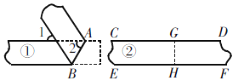
A. 纸带①的边线平行,纸带②的边线不平行 B. 纸带①、②的边线都平行
C. 纸带①的边线不平行,纸带②的边线平行 D. 纸带①、②的边线都不平行
-
科目: 来源: 题型:
查看答案和解析>>【题目】随着“中国诗词大会”节目的热播,《唐诗宋词精选》一书也随之热销.如果一次性购买10本以上,超过10本的那部分书的价格将打折,并依此得到付款金额y(单位:元)与一次性购买该书的数量x(单位:本)之间的函数关系如图所示,则下列结论错误的是( )
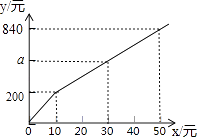
A.一次性购买数量不超过10本时,销售价格为20元/本
B.a=520
C.一次性购买10本以上时,超过10本的那部分书的价格打八折
D.一次性购买20本比分两次购买且每次购买10本少花80元
相关试题

