【题目】如图,在△ABC中,BD⊥AC,AB=6, ![]() ,∠A=30°
,∠A=30° 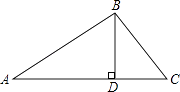
(1)求AD和BC;
(2)求sin∠C.
参考答案:
【答案】
(1)解:在Rt△ABD中,∵∠ADB=90°,AB=6,∠A=30°,
∴BD= ![]() AB=3,AD=
AB=3,AD= ![]() BD=3
BD=3 ![]()
(2)解:∵ ![]() ,AD=3
,AD=3 ![]() ,
,
∴CD=AC﹣AD=2 ![]() .
.
在Rt△CBD中,∵∠CDB=90°,BD=3,CD=2 ![]() ,
,
∴BC= ![]() =
= ![]() ,
,
∴sin∠C= ![]() =
= ![]() =
= ![]()
【解析】(1)在Rt△ABD中,根据含30°角的直角三角形的性质得出BD= ![]() AB=3,AD=
AB=3,AD= ![]() BD=3
BD=3 ![]() ;(2)先求出CD=AC﹣AD=2
;(2)先求出CD=AC﹣AD=2 ![]() ,然后在Rt△CBD中,利用勾股定理求出BC=
,然后在Rt△CBD中,利用勾股定理求出BC= ![]() =
= ![]() ,再根据三角函数的定义即可求出sin∠C的值.
,再根据三角函数的定义即可求出sin∠C的值.
【考点精析】本题主要考查了解直角三角形的相关知识点,需要掌握解直角三角形的依据:①边的关系a2+b2=c2;②角的关系:A+B=90°;③边角关系:三角函数的定义.(注意:尽量避免使用中间数据和除法)才能正确解答此题.
-
科目: 来源: 题型:
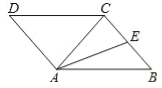
查看答案和解析>>【题目】如图,在ABCD中,AC为对角线,AC=BC=5,AB=6,AE是△ABC的中线.
(1)用无刻度的直尺画出△ABC的高CH(保留画图痕迹);
(2)求△ACE的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】地表以下岩层的温度T(℃)随着所处的深度h(km)的变化而变化,T与h之间在一定范围内近似地成一次函数关系.
(1)根据下表,求T(℃)与h(km)之间的函数关系式;
温度T(℃)
…
90
160
300
…
深度h(km)
…
2
4
8
…
(2)当岩层温度达到1770℃时,岩层所处的深度为多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角坐标系内,一次函数y=kx+b(k<0,b<0)的图象分别与x轴、y轴和直线x=4相交于A,B,C三点,直线x=4与x轴交于点D,四边形OBCD(O是坐标原点)的面积是10,若点A的横坐标是-
 ,求这个一次函数表达式.
,求这个一次函数表达式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】完成下面的推理.
如图,BE平分∠ABD,DE平分∠BDC,且∠α+∠β=90°,试说明:AB∥CD.
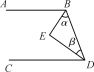
完成推理过程:
∵BE平分∠ABD(已知),
∴∠ABD=2∠α(__________).
∵DE平分∠BDC(已知),
∴∠BDC=2∠β (__________).
∴∠ABD+∠BDC=2∠α+2∠β=2(∠α+∠β)( __________).
∵∠α+∠β=90°(已知),
∴∠ABD+∠BDC=180°(__________).
∴AB∥CD(____________________).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是半圆O的直径,C、D是半圆O上的两点,且OD∥BC,OD与AC交于点E.
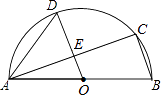
(1)若∠B=70°,求∠CAD的度数;
(2)若AB=4,AC=3,求DE的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知正比例函数y=kx经过点A,点A在第四象限,过点A作AH⊥x轴,垂足为点H,点A的横坐标为3,且△AOH的面积为3.
(1)求正比例函数的解析式;
(2)在x轴上能否找到一点P,使△AOP的面积为5?若存在,求点P的坐标;若不存在,请说明理由.
相关试题

