【题目】如图,AB是半圆O的直径,C、D是半圆O上的两点,且OD∥BC,OD与AC交于点E. 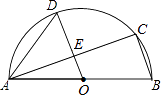
(1)若∠B=70°,求∠CAD的度数;
(2)若AB=4,AC=3,求DE的长.
参考答案:
【答案】
(1)解:∵AB是半圆O的直径,
∴∠ACB=90°,
又∵OD∥BC,
∴∠AEO=90°,即OE⊥AC,
∠CAB=90°﹣∠B=90°﹣70°=20°,∠AOD=∠B=70°.
∵OA=OD,
∴∠DAO=∠ADO= ![]() =
= ![]() =55°
=55°
∴∠CAD=∠DAO﹣∠CAB=55°﹣20°=35°
(2)解:在直角△ABC中,BC= ![]() =
= ![]() =
= ![]() .
.
∵OE⊥AC,
∴AE=EC,
又∵OA=OB,
∴OE= ![]() BC=
BC= ![]() .
.
又∵OD= ![]() AB=2,
AB=2,
∴DE=OD﹣OE=2﹣ ![]()
【解析】(1)根据圆周角定理可得∠ACB=90°,则∠CAB的度数即可求得,在等腰△AOD中,根据等边对等角求得∠DAO的度数,则∠CAD即可求得;(2)易证OE是△ABC的中位线,利用中位线定理求得OE的长,则DE即可求得.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角坐标系内,一次函数y=kx+b(k<0,b<0)的图象分别与x轴、y轴和直线x=4相交于A,B,C三点,直线x=4与x轴交于点D,四边形OBCD(O是坐标原点)的面积是10,若点A的横坐标是-
 ,求这个一次函数表达式.
,求这个一次函数表达式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,BD⊥AC,AB=6,
 ,∠A=30°
,∠A=30° 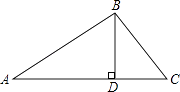
(1)求AD和BC;
(2)求sin∠C. -
科目: 来源: 题型:
查看答案和解析>>【题目】完成下面的推理.
如图,BE平分∠ABD,DE平分∠BDC,且∠α+∠β=90°,试说明:AB∥CD.
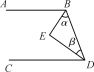
完成推理过程:
∵BE平分∠ABD(已知),
∴∠ABD=2∠α(__________).
∵DE平分∠BDC(已知),
∴∠BDC=2∠β (__________).
∴∠ABD+∠BDC=2∠α+2∠β=2(∠α+∠β)( __________).
∵∠α+∠β=90°(已知),
∴∠ABD+∠BDC=180°(__________).
∴AB∥CD(____________________).
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知正比例函数y=kx经过点A,点A在第四象限,过点A作AH⊥x轴,垂足为点H,点A的横坐标为3,且△AOH的面积为3.
(1)求正比例函数的解析式;
(2)在x轴上能否找到一点P,使△AOP的面积为5?若存在,求点P的坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在读书月活动中,学校准备购买一批课外读物.为使课外读物满足同学们的需求,学校就“我最喜爱的课外读物”从文学、艺术、科普和其他四个类别进行了抽样调查(每位同学只选一类),如图是根
据调查结果绘制的两幅不完整的统计图.

请你根据统计图提供的信息,解答下列问题:
(1)本次调查中,一共调查了 名同学;
(2)条形统计图中,m= ,n= ;
(3)扇形统计图中,艺术类读物所在扇形的圆心角是 度;
(4)学校计划购买课外读物6000册,请根据样本数据,估计学校购买其他类读物多少册比较合理?
-
科目: 来源: 题型:
查看答案和解析>>【题目】中考体育测试满分为40分,某校九年级进行了中考体育模拟测试,随机抽取了部分学生的考试成绩进行统计分析,并把分析结果绘制成如下两幅统计图.试根据统计图中提供的数据,回答下列问题:

(1)抽取的样本中,成绩为39分的人数有人;
(2)抽取的样本中,考试成绩的中位数是分,众数是分;
(3)若该校九年级共有500名学生,试根据这次模拟测试成绩估计该校九年级将有多少名学生能得到满分?
相关试题

