【题目】如图,折叠长方形的一边AD,使点D落在BC边上的点F处,BC=10cm,AB=8cm,求:
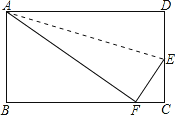
(1)EC的长;
(2)AE的长.
参考答案:
【答案】(1)3cm;(2)![]() cm.
cm.
【解析】
试题分析:(1)首先根据勾股定理求出BF的长,借助翻转变换的性质及勾股定理求出DE的长即可解决问题.
(2)直接根据勾股定理求出AE的长.
试题解析:(1)∵四边形ABCD为长方形,
∴AD=BC=10,DC=AB=8;
由题意得:△ADE≌△AFE,
∴AF=AD=10,EF=ED(设为x),
则EC=8-x;
在直角△ABF中,
由勾股定理得:
BF=![]() =6,
=6,
∴FC=10-6=4;
在直角△EFC中,
由勾股定理得:
x2=42+(8-x)2,
解得:x=5,8-x=3;
∴EC的长为3(cm).
(2)由勾股定理得:
AE=![]() (cm).
(cm).
-
科目: 来源: 题型:
查看答案和解析>>【题目】将两个全等的直角三角形ABC和DBE按图①方式摆放,其中∠ACB=∠DEB=90°,∠A=∠D=30°,点E落在AB上,DE所在直线交AC所在直线于点F.
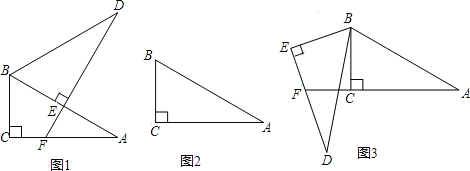
(1)求证:AF+EF=DE;
(2)若将图①中的△DBE绕点B按顺时针方向旋转角α,且0°<α<60°,其它条件不变,请在图②中画出变换后的图形,并直接写出你在(1)中猜想的结论是否仍然成立;
(3)若将图①中的△DBE绕点B按顺时针方向旋转角β,且60°<β<180°,其它条件不变,如图③.你认为(1)中猜想的结论还成立吗?若成立,写出证明过程;若不成立,请写出AF、EF与DE之间的关系,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,正方形网格中,△ABC为格点三角形(即三角形的顶点都在格点上).
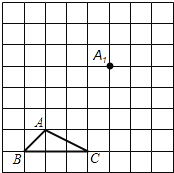
(1)把△ABC沿BA方向平移后,点A移到点A1,在网格中画出平移后得到的△A1B1C1;
(2)把△A1B1C1绕点A1按逆时针旋转90°,在网格中画出旋转后的△A1B2C2;
(3)如果网格中小正方形的变长为1,求点B经过(1)(2)变换的路径总长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,PA,PB切⊙O于A、B两点,CD切⊙O于点E,交PA,PB于C, D.若⊙O的半径为r,△PCD的周长等于3r,则tan∠APB的值是( )

A.
 B.
B. C.
C. D.
D.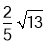
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读材料:求值1+2+22+23+24+…+22014
解:设S=1+2+22+23+24+…+22014 ①,将等式两边同时乘以2得
2S=2+22+23+24+…+22014+22015 ②将②﹣①得:S=22015﹣1,即S=1+2+22+23+24+…+22014=22015﹣1
请你仿照此法计算:(1)1+2+22+23+24+…+210
(2)1+3+32+33+34+…+3n(其中n为正整数)
-
科目: 来源: 题型:
查看答案和解析>>【题目】

(1)请你根据图中A、B两点的位置,分别写出它们所表示的有理数
A: _________ B: _________ ;
(2)观察数轴,与点A的距离为4的点表示的数是:__________ ;
(3)若将数轴折叠,使得A点与-3表示的点重合,则B点与数____表示的点重合;
(4)若数轴上M、N两点之间的距离为2016(M在N的左侧),且M、N两点经过(3)中折叠后互相重合,则M、N两点表示的数分别是:
M: N: .
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列调查中,适宜采用抽样调查方式的是( )
A. 对某班学生体重情况的调查
B. 对某办公室职员年龄的调查
C. 对某班学生每天课余工作时间的调查
D. 对某批次汽车的抗撞击能力的调查
相关试题

