【题目】如图,在平面直角坐标系中,已知矩形ABCD的三个顶点B(1,0),C(3,0),D(3,4).以A为顶点的抛物线y=ax2+bx+c过点C.动点P从点A出发,沿线段AB向点B运动.同时动点Q从点C出发,沿线段CD向点D运动.点P,Q的运动速度均为每秒1个单位.运动时间为t秒.过点P作PE⊥AB交AC于点E.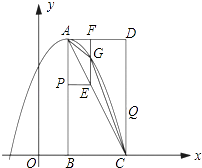
(1)直接写出点A的坐标,并求出抛物线的解析式;
(2)过点E作EF⊥AD于F,交抛物线于点G,当t为何值时,△ACG的面积最大?最大值为多少?
(3)在动点P,Q运动的过程中,当t为何值时,在矩形ABCD内(包括边界)存在点H,使以C,Q,E,H为顶点的四边形为菱形?请直接写出t的值.
参考答案:
【答案】
(1)A(1,4).
由题意知,可设抛物线解析式为y=a(x﹣1)2+4
∵抛物线过点C(3,0),
∴0=a(3﹣1)2+4,
解得,a=﹣1,
∴抛物线的解析式为y=﹣(x﹣1)2+4,即y=﹣x2+2x+3.
(2)解:∵A(1,4),C(3,0),
∴可求直线AC的解析式为y=﹣2x+6.
∵点P(1,4﹣t).
∴将y=4﹣t代入y=﹣2x+6中,解得点E的横坐标为x=1+ ![]() .
.
∴点G的横坐标为1+ ![]() ,代入抛物线的解析式中,可求点G的纵坐标为4﹣
,代入抛物线的解析式中,可求点G的纵坐标为4﹣ ![]() .
.
∴GE=(4﹣ ![]() )﹣(4﹣t)=t﹣
)﹣(4﹣t)=t﹣ ![]() .
.
又∵点A到GE的距离为 ![]() ,C到GE的距离为2﹣
,C到GE的距离为2﹣ ![]() ,
,
即S△ACG=S△AEG+S△CEG= ![]() EG
EG ![]() +
+ ![]() EG(2﹣
EG(2﹣ ![]() )
)
= ![]() 2(t﹣
2(t﹣ ![]() )=﹣
)=﹣ ![]() (t﹣2)2+1.
(t﹣2)2+1.
当t=2时,S△ACG的最大值为1.
(3)解:第一种情况如图1所示,点H在AC的上方, 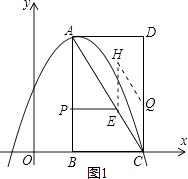
由四边形CQEH是菱形知CQ=CE=t,
根据△APE∽△ABC,知
![]() =
= ![]() ,即
,即 ![]() =
= ![]() ,解得t=20﹣8
,解得t=20﹣8 ![]() ;
;
第二种情况如图2所示,点H在AC的下方, 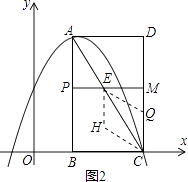
由四边形CQHE是菱形知CQ=QE=EH=HC=t,PE= ![]() t,EM=2﹣
t,EM=2﹣ ![]() t,MQ=4﹣2t.
t,MQ=4﹣2t.
则在直角三角形EMQ中,根据勾股定理知EM2+MQ2=EQ2,即(2﹣ /span>![]() t)2+(4﹣2t)2=t2,
t)2+(4﹣2t)2=t2,
解得,t1= ![]() ,t2=4(不合题意,舍去).
,t2=4(不合题意,舍去).
综上所述,t=20﹣8 ![]() 或t=
或t= ![]() .
.
【解析】(1)由抛物线过点C(3,0),求出抛物线的解析式为y=﹣x2+2x+3;(2)由A(1,4),C(3,0),可求出直线AC的解析式;又点P(1,4﹣t),解得点E的横坐标为x=1+ ![]() ,所以点G的横坐标为1+
,所以点G的横坐标为1+ ![]() ,代入抛物线的解析式中,可求点G的纵坐标为4﹣
,代入抛物线的解析式中,可求点G的纵坐标为4﹣ ![]() ,得到GE=(4﹣
,得到GE=(4﹣ ![]() )﹣(4﹣t)=t﹣
)﹣(4﹣t)=t﹣ ![]() ,又点A到GE的距离为
,又点A到GE的距离为 ![]() ,C到GE的距离为2﹣
,C到GE的距离为2﹣ ![]() ,即S△ACG=S△AEG+S△CEG,求出S△ACG的最大值为;(3)第一种情况如图1所示,点H在AC的上方,由四边形CQEH是菱形知CQ=CE=t,根据△APE∽△ABC
,即S△ACG=S△AEG+S△CEG,求出S△ACG的最大值为;(3)第一种情况如图1所示,点H在AC的上方,由四边形CQEH是菱形知CQ=CE=t,根据△APE∽△ABC![]() ,得到比例,求出t的值;第二种情况如图2所示,点H在AC的下方,由四边形CQHE是菱形知CQ=QE=EH=HC=t,PE=
,得到比例,求出t的值;第二种情况如图2所示,点H在AC的下方,由四边形CQHE是菱形知CQ=QE=EH=HC=t,PE= ![]() t,EM=2﹣
t,EM=2﹣ ![]() t,MQ=4﹣2t.则在直角三角形EMQ中,根据勾股定理知EM2+MQ2=EQ2,求出t的值 ;此题是综合题,难度较大,计算和解方程时需认真仔细.
t,MQ=4﹣2t.则在直角三角形EMQ中,根据勾股定理知EM2+MQ2=EQ2,求出t的值 ;此题是综合题,难度较大,计算和解方程时需认真仔细.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的弦,D为OA半径的中点,过D作CD⊥OA交弦AB于点E,交⊙O于点F,且CE=CB.
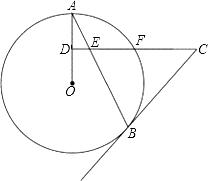
(1)求证:BC是⊙O的切线;
(2)连接AF,BF,求∠ABF的度数;
(3)如果BE=10,sinA=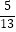 ,求⊙O的半径.
,求⊙O的半径. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中(AB≠BC),直线EF经过其对角线的交点O,且分别交AD,BC于点M,N,交BA,DC的延长线于点E,F,下列结论:①AO=BO;②OE=OF;③△EAM≌△FCN;④△EAO≌△DCO.其中一定正确的是()
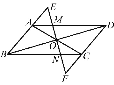
A. ①② B. ②③
C. ①④ D. ①③
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中,分别以AB、AD为边向外作等边△ABE、△ADF,延长CB交AE于点G,点G在点A、E之间,连接CE、CF,EF,则以下四个结论一定正确的是:①△CDF≌△EBC;②∠CDF=∠EAF;③△ECF是等边△;④CG⊥AE( )

A. 只有①② B. 只有①②③ C. 只有③④ D. ①②③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】在同一坐标系中,一次函数y=﹣mx+n2与二次函数y=x2+m的图象可能是( )
A.
B.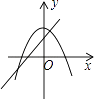
C.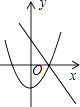
D.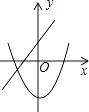
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,直线AB∥CD,E为AB、CD间的一点,连接EA、EC.
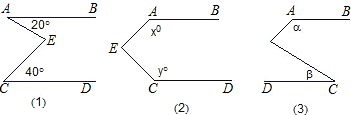
(1)如图①,若∠A=20°,∠C=40°,则∠AEC= °.
(2)如图②,若∠A=x°,∠C=y°,则∠AEC= °.
(3)如图③,若∠A=α,∠C=β,则α,β与∠AEC之间有何等量关系.并简要说明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD的边长为2,BE=CE,MN=1,线段MN的两端点在CD、AD上滑动,当DM为( )时,△ABE与以D、M、N为顶点的三角形相似.
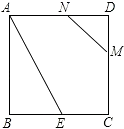
A.
B.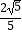
C. 或
或 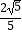
D.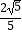 或
或 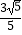
相关试题

