【题目】如图,在平行四边形ABCD中,分别以AB、AD为边向外作等边△ABE、△ADF,延长CB交AE于点G,点G在点A、E之间,连接CE、CF,EF,则以下四个结论一定正确的是:①△CDF≌△EBC;②∠CDF=∠EAF;③△ECF是等边△;④CG⊥AE( )

A. 只有①② B. 只有①②③ C. 只有③④ D. ①②③④
参考答案:
【答案】B
【解析】根据题意,结合图形,对选项一一求证,判定正确选项
解:在□ABCD中,∠ADC=∠ABC,AD=BC,CD=AB,
∵△ABE、△ADF都是等边三角形,
∴AD=DF,AB=EB,∠ADF=∠ABE=60°,
∴DF=BC,CD=BC,
∴∠CDF=360°-∠ADC-60°=300°-∠ADC,
∠EBC=360°-∠ABC-60°=300°-∠ABC,
∴∠CDF=∠EBC,
在△CDF和△EBC中,
DF=BC,∠CDF=∠EBC,CD=EB,
∴△CDF≌△EBC(SAS),故①正确;
在ABCD中,∠DAB=180°-∠ADC,
∴∠EAF=∠DAB+∠DAF+∠BAE=180°-∠ADC+60°+60°=300°-∠ADC,
∴∠CDF=∠EAF,故②正确;
同理可证△CDF≌△EAF,
∴EF=CF,
∵△CDF≌△EBC,
∴CE=CF,
∴EC=CF=EF,
∴△ECF是等边三角形,故③正确;
当CG⊥AE时,∵△ABE是等边三角形,
∴∠ABG=30°,
∴∠ABC=180°-30°=150°,
∵∠ABC=150°无法求出,故④错误;
综上所述,正确的结论有①②③.
故选B.
“点睛”本题考查了全等三角形的判定、等边三角形的判定和性质、平行线的性质等知识,综合性强,考查学生综合运用数学知识的能力.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)a2a3
(2)y14÷y3
(3)(3x2)3
(4)( )5(
)5(  )5
)5
(5)(﹣2)2﹣(π﹣3)0+( )﹣1 .
)﹣1 . -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,有足够多的边长为a的小正方形(A类),长为b宽为a的长方形(B类)以及边长为b的大正方形(C类) ,发现利用图①中的三种材料各若干可以拼出一些长方形来解释某些等式,比如图②可以解释为:(a+2b)(a+b)=a2+3ab+2b2
(1)取图①中的若干个(三种图形都要取到)拼成一个长方形,使其面积为(2a+b)(a+2b),在下面虚框中画出图形,并根据图形回答(2a+b)(a+2b)= .
(2)若取其中的若干个(三种图形都要取到)拼成一个长方形,使其面积为a2+5ab+6b2 . ①你画的图中需C类卡片张.
②可将多项式a2+5ab+6b2分解因式为
(3)如图③,大正方形的边长为m,小正方形的边长为n,若用x、y表示四个相同矩形的两边长(x>y),观察图案并判断,将正确关系式的序号填写在横线上(填写序号) ①xy= ②x+y=m ③x2﹣y2=mn ④x2+y2=
②x+y=m ③x2﹣y2=mn ④x2+y2=  .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,点P(-20,a)与点Q(b , 13)关于原点对称,则a+b的值为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题正确的个数是( )个.
①用四舍五入法按要求对0.05049分别取近似值为0.050(精确到0.001);
②若代数式
 有意义,则x的取值范围是x≤﹣
有意义,则x的取值范围是x≤﹣ 且x≠﹣2;
且x≠﹣2;③数据1、2、3、4的中位数是2.5;
④月球距离地球表面约为384000000米,将这个距离用科学记数法(保留两个有效数字)表示为3.8×108米.
A.1 B.2 C.3 D.4
-
科目: 来源: 题型:
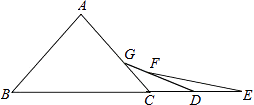
查看答案和解析>>【题目】如图,已知△ABC是等边三角形,点D、E在BC的延长线上,G是AC上一点,且CG=CD,F是GD上一点,且DF=DE,则∠E=度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,点A的横坐标为﹣1,点B在x轴的负半轴上,AB=AO,∠ABO=30°,直线MN经过原点O,点A关于直线MN的对称点A1在x轴的正半轴上,点B关于直线MN的对称点为B1 , 则∠AOM的度数为;点B1的纵坐标为 .

相关试题

