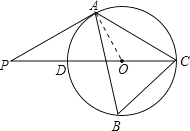
【题目】如图,△ABC内接于⊙O,∠B=60°,CD是⊙O的直径,点P是CD延长线上的一点,且AP=AC.

(1)求证:PA是⊙O的切线;
(2)若PD=![]() ,求⊙O的直径.
,求⊙O的直径.
参考答案:
【答案】(1)证明见解析;(2)⊙O的直径为![]() .
.
【解析】
试题分析:(1)连接OA,根据圆周角定理求出∠AOC,再由OA=OC得出∠ACO=∠OAC=30°,再由AP=AC得出∠P=30°,继而由∠OAP=∠AOC﹣∠P,可得出OA⊥PA,从而得出结论;
(2)利用含30°的直角三角形的性质求出OP=2OA,可得出OP﹣PD=OD,再由PD=![]() ,可得出⊙O的直径.
,可得出⊙O的直径.
(1)证明:连接OA,
∵∠B=60°,
∴∠AOC=2∠B=120°,
又∵OA=OC,
∴∠OAC=∠OCA=30°,
又∵AP=AC,
∴∠P=∠ACP=30°,
∴∠OAP=∠AOC﹣∠P=90°,
∴OA⊥PA,
∴PA是⊙O的切线.
(2)在Rt△OAP中,∵∠P=30°,
∴PO=2OA=OD+PD,
又∵OA=OD,
∴PD=OA,
∵![]() ,
,
∴![]() .
.
∴⊙O的直径为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个角的补角是它的余角的4倍,则这个角是_________度。
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知如图,一次函数y=kx+b的图象与反比例函数
 的图象相交于A、B两点.
的图象相交于A、B两点.
(1)利用图中条件,求反比例函数和一次函数的解析式;
(2)根据图象写出使一次函数的值大于反比例函数的值的x的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AB=AC,AD是△ABC外角的平分线,已知∠BAC=∠ACD.
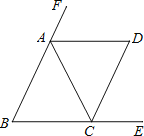
(1)求证:△ABC≌△CDA;
(2)若∠B=60°,求证:四边形ABCD是菱形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某小区准备新建50个停车位,以解决小区停车难的问题.已知新建1个地上停车位和1个地下停车位共需0.5万元;新建3个地上停车位和2个地下停车位共需1.1万元.
(1)该小区新建1个地上停车位和1个地下停车位各需多少万元?
(2)若该小区预计投资金额超过10万元,且地上的停车位要求不少于30个,问共有几种建造方案?
(3)对(2)中的几种建造方案中,哪一个方案的投资最少?并求出最少投资金额.
-
科目: 来源: 题型:
查看答案和解析>>【题目】P点在平面直角坐标系的第二象限,P到x轴的距离为1,到y轴的距离为2,则P点的坐标是( )
A. (-1,2) B. (-2,1) C. (1,-2) D. (2,-1)
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个数若有两个不同的平方根,则这两个平方根的和为( )
A. 大于0 B. 等于0 C. 小于0 D. 不能确定
相关试题

