Question

【题目】某校规划在一块长AD为18m，宽AB为13m的长方形场地ABCD上，设计分别与AD，AB平行的横向通道和纵向通道，其余部分铺上草皮．

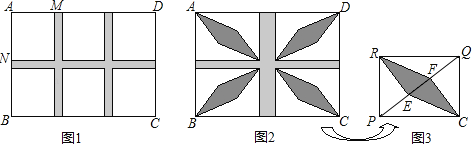
（1）如图1，若设计三条通道，一条横向，两条纵向，且它们的宽度相等，其余六块草坪相同，其中一块草坪两边之比AM：AN=8：9，问通道的宽是多少？

（2）为了建造花坛，要修改（1）中的方案，如图2，将三条通道改为两条通道，纵向的宽度改为横向宽度的2倍，其余四块草坪相同，且每一块草坪均有一边长为8m，这样能在这些草坪建造花坛．如图3，在草坪RPCQ中，已知RE⊥PQ于点E，CF⊥PQ于点F，求花坛RECF的面积．

Answer 1

【答案】（1）通道的宽是1m；（2）花坛RECF的面积为13.44m2．

【解析】

试题分析：（1）利用AM：AN=8：9，设通道的宽为xm，AM=8ym，则AN=9y，进而利用AD为18m，宽AB为13m得出等式求出即可；

（2）根据题意得出纵向通道的宽为2m，横向通道的宽为1m，进而得出PQ，RE的长，即可得出PE、EF的长，进而求出花坛RECF的面积．

解：（1）设通道的宽为xm，AM=8ym，

∵AM：AN=8：9，

∴AN=9y，

∴，

解得：．

答：通道的宽是1m；

（2）∵四块相同草坪中的每一块，有一条边长为8m，若RP=8，则AB＞13，不合题意，

∴RQ=8，

∴纵向通道的宽为2m，横向通道的宽为1m，

∴RP=6，

∵RE⊥PQ，四边形RPCQ是长方形，

∴PQ=10，

∴RE×PQ=PR×QR=6×8，

∴RE=4.8，

∵RP2=RE2+PE2，

∴PE=3.6，

同理可得：QF=3.6，

∴EF=2.8，

∴S四边形RECF=4.8×2.8=13.44，

即花坛RECF的面积为13.44m2．