【题目】在一个不透明的口袋里装有只有颜色不同的黑、白两种颜色的球20个,某学习小组做摸球实验,将球搅匀后从中随机摸出一个记下颜色,再把它放回口袋中,不断重复,如表是活动进行中的一组数据统计:
摸球的次数m | 100 | 150 | 200 | 500 | 800 | 1000 |
摸到白球的次数n | 58 | 96 | 116 | 295 | 484 | 601 |
摸到白球的频率 | 0.58 | 0.64 | 0.58 | 0.59 | 0.605 | 0.601 |
(1)请估计:当n很大时,摸到白球的频率将会接近________ ;
(2)假如你去摸一次,你摸到白球的概率是________,摸到黑球的概率是________;
(3)试估算口袋中黑球有________个,白球有________个.
参考答案:
【答案】 0.60 0.60 0.40 8 12
【解析】试题分析:(1)当n很大时,摸到白球的频率将会接近表格中频率的平均数,求出平均数即可;
(2)根据(1)中求得的摸到白球的频率即可得;
(3)用球的总个数乘以各自的频率即可求得球的个数.
试题解析:(1)当n很大时,摸到白球的频率将会接近(0.58+0.64+0.58+0.59+0.605+0.601)÷6≈0.60,
故答案为:0.60;
(2)摸到白球的概率是0.60,摸到黑球的概率是1-0.60=0.40,
故答案为:0.60,0.40;
(3)白球有20×0.60=12(只),黑球有20-12=8(只),
故答案为:8,12.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)在下列两个条件下,分别求代数式
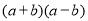 和
和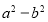 的值,将结果直接填写在下面的横线上:
的值,将结果直接填写在下面的横线上:①当
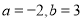 时,
时,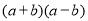 = ,
= ,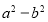 = ;
= ;②当
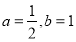 时,
时,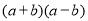 = ,
= ,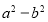 = ;
= ;(2)观察结果,你有什么发现?请写出结论,并再任选a、b的值加以验证;
(3)利用你的发现,求
 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】我市某中学举行“中国梦校园好声音”歌手大赛,高、初中部根据初赛成绩,各选出5名选手组成初中代表队和高中代表队参加学校决赛。两个队各选出的5名选手的决赛成绩如图所示.
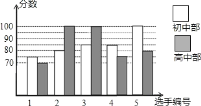
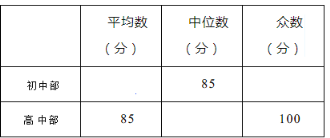
(1)根据图示填写下表;
(2)结合两队成绩的平均数和中位数,分析哪个队的决赛成绩较好;
(3)计算两队决赛成绩的方差并判断哪一个代表队选手成绩较为稳定.
-
科目: 来源: 题型:
查看答案和解析>>【题目】出租车司机小李某天上午营运时是在东西走向的大街上进行的,如果规定向东为正,向西为负,他这天上午所接六位乘客的行车里程(单位:
 )如下:
)如下: ,
, ,
, ,
, ,
, ,
, ,
,问:(1)将最后一位乘客送到目的地时,小李在什么位置?
(2)若汽车耗油量为
 (升/千米),这天上午小李接送乘客,出租车共耗油多少升?
(升/千米),这天上午小李接送乘客,出租车共耗油多少升?(3)若出租车起步价为8元,起步里程为
 (包括
(包括 ),超过部分每千米1.2元,问小李这天上午共得车费多少元?
),超过部分每千米1.2元,问小李这天上午共得车费多少元? -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:在平面直角坐标系中A(0,a)、B(b,0),且满足4(a﹣2)2+
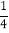 (b﹣4)2=0,点P(m,m)在线段AB上
(b﹣4)2=0,点P(m,m)在线段AB上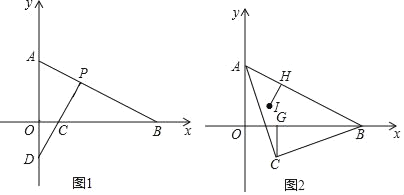
(1)求A、B的坐标;
(2)如图1,若过P作PC⊥AB交x轴于C,交y轴交于点D,求
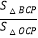 的值;
的值;(3)如图2,以AB为斜边在AB下方作等腰直角△ABC,CG⊥OB于G,设I是∠OAB的角平分线与OP的交点,IH⊥AB于H.请探究
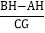 的值是否发生改变,若不改变请求其值;若改变请说明理由.
的值是否发生改变,若不改变请求其值;若改变请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】两个反比例函数y=
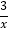 ,y=
,y=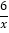 在第一象限内的图象如图所示,点P1,P2,P3,....,P99,在反比例函数y=
在第一象限内的图象如图所示,点P1,P2,P3,....,P99,在反比例函数y=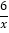 图象上,它们的横坐标分别是x1,x2,x3,....,x99,纵坐标分别是1,3,5,·…·,共99个连续奇数过点P1,P2,P3,…,P99分别作y轴的平行线线,与y=
图象上,它们的横坐标分别是x1,x2,x3,....,x99,纵坐标分别是1,3,5,·…·,共99个连续奇数过点P1,P2,P3,…,P99分别作y轴的平行线线,与y=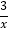 的图象交点依次是Q1(x1,y1),Q2(x2,y2),Q3(x3,y3),.....,Q99(x99,y99),则y99=______
的图象交点依次是Q1(x1,y1),Q2(x2,y2),Q3(x3,y3),.....,Q99(x99,y99),则y99=______
-
科目: 来源: 题型:
查看答案和解析>>【题目】同学们学过有理数减法可以转化为有理数加法来运算,有理数除法可以转化为有理数乘法来运算.其实这种转化的数学方法,在学习数学时会经常用到,通过转化我们可以把一个复杂问题转化为一个简单问题来解决.
例如:计算

此题我们按照常规的运算方法计算比较复杂,但如果采用下面的方法把乘法转化为减法后计算就变得非常简单.
分析方法:
因为
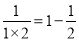 ,
,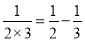 ,
,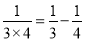 ,
, ,
,所以,将以上4个等式两边分别相加即可得到结果,解法如下:
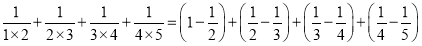
=
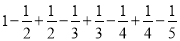
=
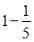
=
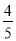
(1)
 =
= (2)应用上面的方法计算:
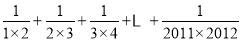 ;
;(3)类比应用上面的方法探究并计算:
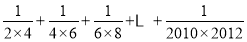
相关试题

