【题目】如图,在△ABC中,∠BAC=90°,AB=6cm,BC=10cm,点D在线段AC上,且CD=2cm,动点P从BA的延长线上距A点10cm的E点出发,以每秒2cm的速度沿射线EA的方向运动了 ![]() 秒。
秒。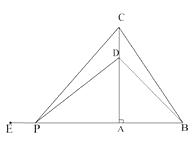
(1)求AD的长;
(2)直接写出用含有 ![]() 的代数式表示PE=;
的代数式表示PE=;
(3)在运动过程中,是否存在某个时刻,使△ABC与△ADP全等?若存在,请求出 ![]() 值;若不存在,请说明理由.
值;若不存在,请说明理由.
参考答案:
【答案】
(1)解:∵∠BAC=90°,AB=6cm,BC=10cm,
∴AC= ![]() =8cm,
=8cm,
∵CD=2cm,
∴AD=6cm。
(2)2t
(3)解:存在;当△ABC≌△ADP时AP=AC=8cm
∴PE=10-8=2 cm
∴t=1
当△ABC≌△APD时AP=AB=6 cm
∴PE=10-6=4 cm
∴t=4
【解析】解:(2)因为动点P从BA延长线上距A点10cm的E点出发,以每秒2cm的速度沿射线EA的方向运动了t秒,所以PE=2t。在三角形BAC中用勾股定理可求AC的长,则AD=AC-CD;(2)用含有 t 的代数式表示PE=2t;(3)存在。理由略。
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点A(-2,4),则点A关于y轴对称的点的坐标为__________
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,将三角形各点的横坐标都乘﹣1,纵坐标保持不变,所得图形与原图形相比有怎样的位置关系________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线
 经过点A(-4,0),B(2,0)且与
经过点A(-4,0),B(2,0)且与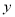 轴交于点C.
轴交于点C.(1)求抛物线的解析式;
(2)如图1,P为线段AC上一点,过点P作
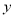 轴平行线,交抛物线于点D,当△ADC的面积最大时,求点P的坐标;
轴平行线,交抛物线于点D,当△ADC的面积最大时,求点P的坐标;(3)如图2,抛物线顶点为E,EF⊥x轴子F点,M、N分别是
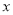 轴和线段EF上的动点,设M的坐标为(m,0),若∠MNC=90°,请指出实数m的变化范围,并说明理由.
轴和线段EF上的动点,设M的坐标为(m,0),若∠MNC=90°,请指出实数m的变化范围,并说明理由.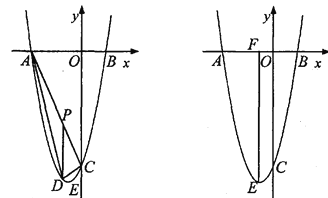
图1 图2
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点D,E,F分别为△ABC各边的中点,下列说法正确的是( )
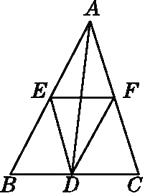
A.DE=DF
B.EF= AB
AB
C.S△ABD=S△ACD
D.AD平分∠BAC -
科目: 来源: 题型:
查看答案和解析>>【题目】某经销店经销一种建筑材料,当每吨售价为260元时,月销售量为45吨.该经销店为提高经营利润,准备采取降价的方式进行促销.经市场调查发现:当每吨售价每下降10元时,月销售量就会增加7.5吨.综合考虑各种因素,每售出一吨建筑材料共需成本及其它费用100元.设每吨材料售价为x(元),该经销店的月利润为y(元).
(1)求出y与x的函数关系式(不要求写出x的取值范围);
(2)该经销店要获得最大月利润,售价应定为每吨多少元;
(3)小王说:“当月利润最大时,月销售额也最大.”你认为对吗?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】用四舍五人法按要求对0.05802分别取近似值得到下列结果,其中错误的是( )
A.0.1(精确到0.1)B.0.06(精确到百分位)
C.0.058(精确到千分位)D.0.058(精确到0.0001)
相关试题

