【题目】在数学兴趣小组活动中,小明进行数学探究活动,将边长为 ![]() 的正方形ABCD与边长为2的正方形AEFG按图1位置放置,AD与AE在同一直线l上,AB与AG在同一直线上.
的正方形ABCD与边长为2的正方形AEFG按图1位置放置,AD与AE在同一直线l上,AB与AG在同一直线上.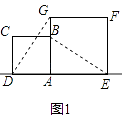
(1)图1中,小明发现DG=BE,请你帮他说明理由.
(2)小明将正方形ABCD按如图2那样绕点A旋转一周,旋转到当点C恰好落在直线l上时,请你直接写出此时BE的长.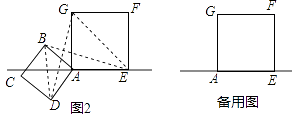
参考答案:
【答案】
(1)解:如图1, 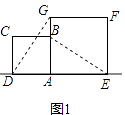 ∵四边形ABCD与四边形AEFG都是正方形,
∵四边形ABCD与四边形AEFG都是正方形,
∴AD=AB,AG=AE,∠DAG=∠BAE=90°.
在△DAG与△BAE中,
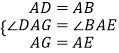 ,
,
∴△DAG≌△BAE,
∴DG=BE;
(2)解:将正方形ABCD按如图2那样绕点A旋转一周,旋转到当点C恰好落在直线l上时,分两种情况:
①如果C在EA的延长线上时,
如备用图1, 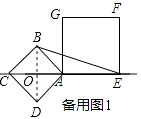
连结BD交AC于O,
∵正方形ABCD边长为 ![]() ,
,
∴BD=AC= ![]() AB=2,AC⊥BD,
AB=2,AC⊥BD,
∴OB=OA= ![]() BD=1.
BD=1.
∵正方形AEFG边长为2,
∴OE=OA+AE=1+2=3.
在Rt△BOE中,∵∠BOE=90°,
∴BE= ![]() =
= ![]() =
= ![]() ;
;
②如果C在AE上时,
如备用图2, 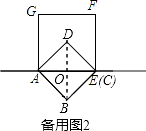
连结BD交AC于O,
∵正方形ABCD边长为 ![]() ,
,
∴BC=AC= ![]() AB=2,
AB=2,
∵正方形AEFG边长为2,
∴AE=2,
∴C与E重合,
∴BE=BC= ![]() .
.
故所求BE的长为 ![]() 或
或 ![]() .
.
【解析】(1)由正方形的性质可判定△DAG≌△BAE,得出DG=BE;(2)C恰好落在直线l上分两类:C在EA的延长线上;C在AE上时;可由勾股定理和正方形的性质求出.
【考点精析】本题主要考查了图形的旋转的相关知识点,需要掌握每一个点都绕旋转中心沿相同方向转动了相同的角度,任意一对对应点与旋转中心的连线所成的角都是旋转角,对应点到旋转中心的距离相等.旋转的方向、角度、旋转中心是它的三要素才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】南博汽车城销售某种型号的汽车,每辆进货价为25万元,市场调研表明:当销售价为29万元时,平均每周能售出8辆,而当销售价每降低0.5万元时,平均每周能多售出4辆.如果设每辆汽车降价x万元,每辆汽车的销售利润为y万元.(销售利润=销售价﹣进货价)

(1)求y与x的函数关系式;在保证商家不亏本的前提下,写出x的取值范围;
(2)假设这种汽车平均每周的销售利润为z万元,试写出z与x之间的函数关系式;
(3)当每辆汽车的定价为多少万元时,平均每周的销售利润最大,最大利润是多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图在4个均由16个小正方形组成的网格正方形中,各有一个格点三角形,那么这4个正方形中,与众不同的是_________,不同之处:______________.


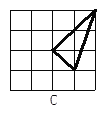

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是小华利用含30°角的三角板测量楼房高度的示意图,已知桌子高AB为1米,地面上B和D之间的距离为100米,则楼高CD约为( )

A.51米
B.59米
C.88米
D.174米 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,已知点A(2,3),点B(﹣2,1),在x轴上存在点P到A,B两点的距离之和最小,则P点的坐标是 .
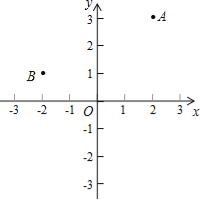
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,抛物线y=x2+bx+c与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C,点B的坐标为(3,0),将直线y=kx沿y轴向上平移3个单位长度后恰好经过B,C两点.
(1)求直线BC及抛物线的解析式;
(2)设抛物线的顶点为D,点P在抛物线的对称轴上,且∠APD=∠ACB,求点P的坐标;
(3)连接CD,求∠OCA与∠OCD两角和的度数. -
科目: 来源: 题型:
查看答案和解析>>【题目】列方程解应用题:
甲列车从A地开往B地,每小时行驶60千米,乙列车同时从B地开往A地,每小时行驶90千米.已知A,B两地相距200km.
(1)经过多长时间两车相遇;
(2)两车相遇的地方离A地多远?
相关试题

