【题目】在平面直角坐标系xOy中,抛物线y=x2+bx+c与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C,点B的坐标为(3,0),将直线y=kx沿y轴向上平移3个单位长度后恰好经过B,C两点.
(1)求直线BC及抛物线的解析式;
(2)设抛物线的顶点为D,点P在抛物线的对称轴上,且∠APD=∠ACB,求点P的坐标;
(3)连接CD,求∠OCA与∠OCD两角和的度数.
参考答案:
【答案】
(1)解:∵y=kx沿y轴向上平移3个单位长度后经过y轴上的点C, 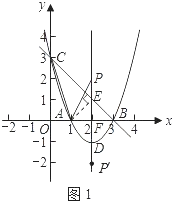
∴C(0,3).
设直线BC的解析式为y=kx+3.
∵B(3,0)在直线BC上,
∴3k+3=0.
解得k=﹣1.
∴直线BC的解析式为y=﹣x+3.
∵抛物线y=x2+bx+c过点B,C,
∴ ![]()
解得 ![]() ,
,
∴抛物线的解析式为y=x2﹣4x+3.
(2)解:由y=x2﹣4x+3.
可得D(2,﹣1),A(1,0).
∴OB=3,OC=3,OA=1,AB=2.
可得△OBC是等腰直角三角形,
∴∠OBC=45°,CB=3 ![]() .
.
如图1,设抛物线对称轴与x轴交于点F,
∴AF= ![]() AB=1.
AB=1.
过点A作AE⊥BC于点E.
∴∠AEB=90度.
可得BE=AE= ![]() ,CE=2
,CE=2 ![]() .
.
在△AEC与△AFP中,∠AEC=∠AFP=90°,∠ACE=∠APF,
∴△AEC∽△AFP.
∴ ![]() ,
, ![]() .
.
解得PF=2.∵点P在抛物线的对称轴上,
∴点P的坐标为(2,2)或(2,﹣2).
(3)解:解法一:
如图2, 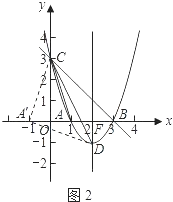
作点A(1,0)关于y轴的对称点A',则A'(﹣1,0).
连接A'C,A'D,
可得A'C=AC= ![]() ,∠OCA'=∠OCA.
,∠OCA'=∠OCA.
由勾股定理可得CD2=20,A'D2=10.
又∵A'C2=10,
∴A'D2+A'C2=CD2.
∴△A'DC是等腰直角三角形,∠CA'D=90°,
∴∠DCA'=45度.
∴∠OCA'+∠OCD=45度.
∴∠OCA+∠OCD=45度.
即∠OCA与∠OCD两角和的度数为45度.
解法二:
如图3,连接BD. 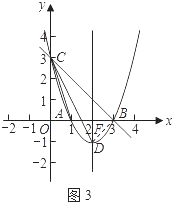
同解法一可得CD= ![]() ,AC=
,AC= ![]() .
.
在Rt△DBF中,∠DFB=90°,BF=DF=1,
∴DB= ![]() .
.
在△CBD和△COA中, ![]() ,
, ![]() ,
, ![]() .
.
∴ ![]() .
.
∴△CBD∽△COA.
∴∠BCD=∠OCA.
∵∠OCB=45°,
∴∠OCA+∠OCD=45度.
即∠OCA与∠OCD两角和的度数为45度.
【解析】直线y=kx向上平移3个单位与y轴交于C,可知C(0,3)代入抛物线解析式即可求出b、c;(2)由∠APD=∠ACB可构造△AEC∽△AFP,由对应边成比例可求出PF,进而求出P坐标;(3)求两角和可转化某一个角然后这两者再相加组成一个角,可由△CBD∽△COA可得出 ∠BCD=∠OCA,∠OCA+∠OCD=∠BCD=45度.
【考点精析】解答此题的关键在于理解相似三角形的判定与性质的相关知识,掌握相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是小华利用含30°角的三角板测量楼房高度的示意图,已知桌子高AB为1米,地面上B和D之间的距离为100米,则楼高CD约为( )

A.51米
B.59米
C.88米
D.174米 -
科目: 来源: 题型:
查看答案和解析>>【题目】在数学兴趣小组活动中,小明进行数学探究活动,将边长为
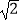 的正方形ABCD与边长为2的正方形AEFG按图1位置放置,AD与AE在同一直线l上,AB与AG在同一直线上.
的正方形ABCD与边长为2的正方形AEFG按图1位置放置,AD与AE在同一直线l上,AB与AG在同一直线上.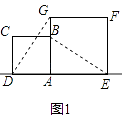
(1)图1中,小明发现DG=BE,请你帮他说明理由.
(2)小明将正方形ABCD按如图2那样绕点A旋转一周,旋转到当点C恰好落在直线l上时,请你直接写出此时BE的长.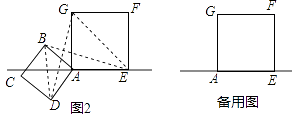
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,已知点A(2,3),点B(﹣2,1),在x轴上存在点P到A,B两点的距离之和最小,则P点的坐标是 .
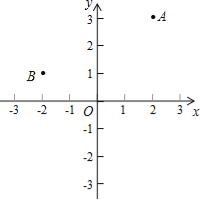
-
科目: 来源: 题型:
查看答案和解析>>【题目】列方程解应用题:
甲列车从A地开往B地,每小时行驶60千米,乙列车同时从B地开往A地,每小时行驶90千米.已知A,B两地相距200km.
(1)经过多长时间两车相遇;
(2)两车相遇的地方离A地多远?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,比例规是一种画图工具,它由长度相等的两脚AC和BD交叉构成,利用它可以把线段按一定的比例伸长或缩短.如果把比例规的两脚合上,使螺丝钉固定在刻度3的地方(即同时使OA=3OC,OB=3OD),然后张开两脚,使A,B两个尖端分别在线段a的两个端点上,当CD=1.8cm时,则AB的长为( )
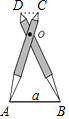
A.7.2 cm
B.5.4 cm
C.3.6 cm
D.0.6 cm -
科目: 来源: 题型:
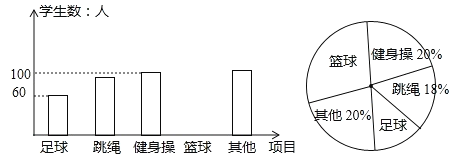
查看答案和解析>>【题目】某市为提高学生参与体育活动的积极性,围绕“你喜欢的体育运动项目(只写一项)”这一问题,对初一新生进行随机抽样调查.下面是根据调查结果绘制成的统计图(不完整).
请你根据图中提供的信息解答下列问题:
(1)本次抽样调查一共调查调查了多少名学生?
(2)根据条形统计图中的数据,求扇形统计图中“最喜欢足球运动”的学生数对应扇形的圆心角度数.
(3)请将条形图补充完整.
(4)若该市2017年约有初一新生21000人,请你估计全市本届学生中“最喜欢足球运动”的学生有多少人?
相关试题

