【题目】南博汽车城销售某种型号的汽车,每辆进货价为25万元,市场调研表明:当销售价为29万元时,平均每周能售出8辆,而当销售价每降低0.5万元时,平均每周能多售出4辆.如果设每辆汽车降价x万元,每辆汽车的销售利润为y万元.(销售利润=销售价﹣进货价)
(1)求y与x的函数关系式;在保证商家不亏本的前提下,写出x的取值范围;
(2)假设这种汽车平均每周的销售利润为z万元,试写出z与x之间的函数关系式;
(3)当每辆汽车的定价为多少万元时,平均每周的销售利润最大,最大利润是多少?
参考答案:
【答案】
(1)解:由题意得:
y=29﹣25﹣x,
∴y=﹣x+4(0≤x≤4);
(2)解:z=(8+ ![]() ×4)y
×4)y
=(8x+8)(﹣x+4)
∴z=﹣8x2+24x+32
=﹣8(x﹣ ![]() )2+50
)2+50
(3)解:由第二问的关系式可知:当x= ![]() 时,z最大=50
时,z最大=50
∴当定价为29﹣1.5=27.5万元时,有最大利润,最大利润为50万元
或:当 ![]()
z最大值= ![]()
∴当定价为29﹣1.5=27.5万元时,有最大利润,最大利润为50万元.
【解析】(1) 单车利润=售价-进价;(2)总利润=单车利润![]() 销量;用x的代数式分别表示单车利润和销量二者相乘;(3)二次函数的最值可通过配方法求出.
销量;用x的代数式分别表示单车利润和销量二者相乘;(3)二次函数的最值可通过配方法求出.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,
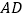 平分
平分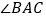 ,
,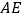 ⊥
⊥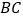 ,∠B=450,∠C=730.
,∠B=450,∠C=730. (1) 求
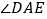 的度数;
的度数;(2) 如图②,若把“
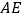 ⊥
⊥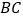 ”变成“点F在DA的延长线上,
”变成“点F在DA的延长线上,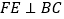 ”,其它条件不变,求
”,其它条件不变,求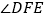 的度数;
的度数;(3) 如图③,若把“
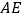 ⊥
⊥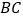 ”变成“
”变成“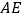 平分
平分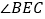 ”,其它条件不变,
”,其它条件不变,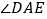 的大小是否变化,并请说明理由.
的大小是否变化,并请说明理由.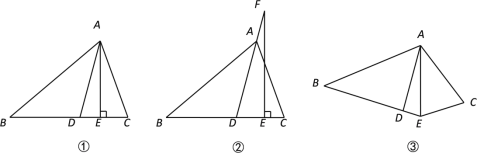
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,线段AC=6,线段BC=15,点M是AC的中点,在CB上取一点N,使得CN:NB=1:2,求MN的长.
解:∵M是AC的中点,AC=6,
∴MC=
 ______(填线段名称)=______,
______(填线段名称)=______,又因为CN:NB=1:2,BC=15,
∴CN=
 ______(填线段名称)=______.
______(填线段名称)=______.∴MN=______(填线段名称)+______(填线段名称)=8
∴MN的长为8.
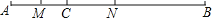
-
科目: 来源: 题型:
查看答案和解析>>【题目】在等边△ABC外侧作直线AP,点B关于直线AP的对称点为D,连结BD,CD,其中CD交直线AP与点E.
(1)如图1,若∠PAB=30°,则∠ACE= ;
(2)如图2,若60°<∠PAB<120°,请补全图形,判断由线段AB,CE,ED可以构成一个含有多少度角的三角形,并说明理由.

-
科目: 来源: 题型:
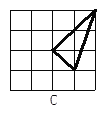
查看答案和解析>>【题目】如图在4个均由16个小正方形组成的网格正方形中,各有一个格点三角形,那么这4个正方形中,与众不同的是_________,不同之处:______________.



-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是小华利用含30°角的三角板测量楼房高度的示意图,已知桌子高AB为1米,地面上B和D之间的距离为100米,则楼高CD约为( )

A.51米
B.59米
C.88米
D.174米 -
科目: 来源: 题型:
查看答案和解析>>【题目】在数学兴趣小组活动中,小明进行数学探究活动,将边长为
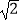 的正方形ABCD与边长为2的正方形AEFG按图1位置放置,AD与AE在同一直线l上,AB与AG在同一直线上.
的正方形ABCD与边长为2的正方形AEFG按图1位置放置,AD与AE在同一直线l上,AB与AG在同一直线上.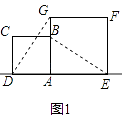
(1)图1中,小明发现DG=BE,请你帮他说明理由.
(2)小明将正方形ABCD按如图2那样绕点A旋转一周,旋转到当点C恰好落在直线l上时,请你直接写出此时BE的长.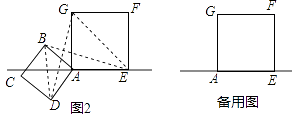
相关试题

