【题目】如图,在△ABC中,已知AB=AC,∠BAC=90°,BC=6cm,直线CM⊥BC,动点D从点C开始沿射线CB方向以每秒2厘米的速度运动,动点E也同时从点C开始在直线CM上以每秒1厘米的速度运动,连接AD、AE,设运动时间为t秒. 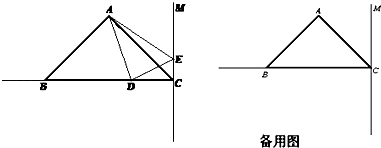
(1)求AB的长;
(2)当t为多少时,△ABD的面积为6cm2?
(3)当t为多少时,△ABD≌△ACE,并简要说明理由.(可在备用图中画出具体图形)
参考答案:
【答案】
(1)解:∵在△ABC中,AB=AC,∠BAC=90°,
∴2AB2=BC2,
∴AB= ![]() =3
=3 ![]() cm;
cm;
(2)解:过A作AF⊥BC交BC于点F,则AF= ![]() BC=3cm,
BC=3cm,
∵S△ABD=6cm2,
∴AF×BD=12,
∴BD=4cm.
若D在B点右侧,则CD=2cm,t=1s;
若D在B点左侧,则CD=10cm,t=5s.
(3)解:动点E从点C沿射线CM方向运动2秒或当动点E从点C沿射线CM的反向延长线方向运动6秒时,△ABD≌△ACE.
理由如下:(说理过程简要说明即可)
①当E在射线CM上时,D必在CB上,则需BD=CE.
∵CE=t,BD=6﹣2t∴t=6﹣2t∴t=2
证明:∵AB=AC,∠B=∠ACE=45°,BD=CE,
∴△ABD≌△ACE.
②当E在CM的反向延长线上时,D必在CB延长线上,则需BD=CE.
∵CE=t,BD=2t﹣6∴t=2t﹣6∴t=6
证明:∵AB=AC,∠ABD=∠ACE=135°,BD=CE
∴△ABD≌△ACE.
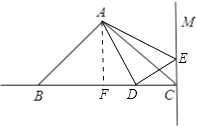
【解析】(1)运用勾股定理直接求出;(2)首先求出△ABD中BD边上的高,然后根据面积公式列出方程,求出BD的值,分两种情况分别求出t的值;(3)假设△ABD≌△ACE,根据全等三角形的对应边相等得出BD=CE,分别用含t的代数式表示CE和BD,得到关于t的方程,从而求出t的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】以长为5cm, 4cm, 7cm的三条线段中的的两条为边,另一条为对角线画平行四边形,可以画出形状不同的平行四边形的个数是 ( )
A. 1 B. 2 C. 3 D. 4
-
科目: 来源: 题型:
查看答案和解析>>【题目】用科学记数法表示660 000的结果是
A.66×104 B.6.6×105 C. 0.66×106 D.6.6×106
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算正确的是( )
A. 3a+2a=a5B. a2a3=a6
C. a3÷a2=aD. (a+b)2=a2+b2
-
科目: 来源: 题型:
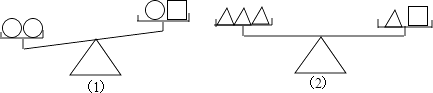
查看答案和解析>>【题目】设“○”、“□”、“△”分别表示三种不同的物体,用天平比较它们质量的大小,两次情况如图所示,那么每个“○”、“□”、“△”这样的物体,按质量从小到大的顺序排列为( )
A.○□△
B.○△□
C.□○△
D.△□○ -
科目: 来源: 题型:
查看答案和解析>>【题目】因式分解:
(1)a(x﹣y)﹣b(y﹣x)
(2)3ax2﹣12ay2
(3)(x+y)2+4(x+y+1) -
科目: 来源: 题型:
查看答案和解析>>【题目】解方程与不等式
(1)解方程组: ;
;
(2)解不等式组: .
.
相关试题

