【题目】小龙在学校组织的社会调查活动中负贵了解他所居住的小区450户居民的家庭收入情况从中随机调查了40户居民家庭收入情况(收入取整数,单位:元),并绘制了如下的频数分布表和频分布直方图。

分组 | 频数 | 百分比 |
600≤ | 2 | 5% |
800≤ | 6 | 15% |
1000≤ | 45% | |
9 | 22.5% | |
1400≤ | ||
1600≤ | 2 | |
合计 | 40 | 100% |
根据以上提供的信息,解答下列问题
(1)补全频数分布表
(2)补全频数分布直方图
(3)请你估计该居民小区家庭属于中等收入(大于1000不足1600元)的大约有多少户
参考答案:
【答案】(1)18,1200≤![]() <1400,3,7.5%,5%;(2)见解析;(3) 338
<1400,3,7.5%,5%;(2)见解析;(3) 338
【解析】
(1)根据1000≤![]() <1200所占的百分比,计算1000≤
<1200所占的百分比,计算1000≤![]() <1200频数即可;再根据总数即可计算出1400≤
<1200频数即可;再根据总数即可计算出1400≤![]() <1600的频数,进而计算百分比.
<1600的频数,进而计算百分比.
(2)根据频数表补充分布直方图即可.
(3)首先计算出大于1000不足1600元所占的百分比,再根据总数计算即可.
解:
(1)4![]() ,
,
根据直方图可得1200≤![]() <1400,
<1400,
![]() ,
,
![]() ,
,
![]()
(2)根据频数表补充如下:
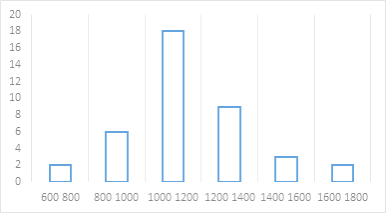
(3)450×75%=338
估计该居民小区家庭属于中等收入(大于1000不足1600元)的大约有338户
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校在“数学小论文”评比活动中,共征集到论文100篇,对论文评比的分数(分数为整数)整理后,分组画出频数分布直方图(如图),已知从左到右5个小长方形的高的比为l:3:7:6:3,那么在这次评比中被评为优秀的论文(分数大于或等于80分为优秀)有____篇.

-
科目: 来源: 题型:
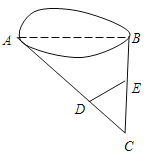
查看答案和解析>>【题目】如图,点D、E分别在AC、BC上,如果测得CD=20m,CE=40m,AD=100m,BE=20m,DE=45m,求A、B两地间的距离。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB∥CD,∠ABK的角平分线BE的反向延长线和∠DCK的角平分线CF的反向延长线交于点H,∠K﹣∠H=27°,则∠K=( )
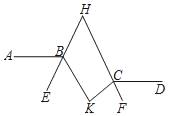
A. 76° B. 78° C. 80° D. 82°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 中,已知点
中,已知点 分别为
分别为 的中点
的中点 ,且
,且 的面积为18,则
的面积为18,则 的面积为____________.
的面积为____________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】用一个直径为10cm的玻璃球和一个圆锥形的牛皮纸纸帽制作一个不倒翁玩具,不倒翁的轴截面如图所示,圆锥的母线AB与⊙O相切于点B,不倒翁的顶点A到桌面L的最大距离是18cm.若将圆锥形纸帽表面全涂上颜色,则涂色部分的面积为_____cm2.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,Rt△OAB的顶点A在x轴的正半轴上,顶点B的坐标为(3,
 ),点C的坐标为(1,0),点P为斜边OB上的一动点,则PA+PC的最小值_____.
),点C的坐标为(1,0),点P为斜边OB上的一动点,则PA+PC的最小值_____.
相关试题

