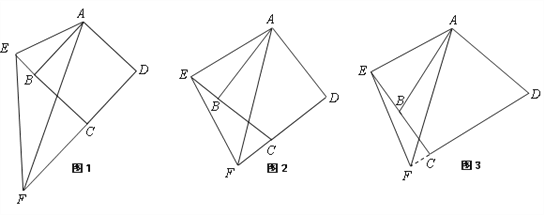
【题目】如图1,四边形ABCD,将顶点为A的角绕着顶点A顺时针旋转,若角的一条边与DC的延长线交于点F,角的另一条边与CB的延长线交于点E,连接EF.
●特例发现 若四边形ABCD为正方形,当∠EAF=45°时,则EF、DF、BE满足数量关系为 ;
●深入探究 如图2,如果在四边形ABCD中,AB=AD,∠ABC=∠ADC=90°,当∠EAF=![]() ∠BAD时,则EF、DF、BE满足数量关系为 ;
∠BAD时,则EF、DF、BE满足数量关系为 ;
如图3,如果四边形ABCD中,AB=AD,∠ABC与∠ADC互补,当∠EAF=![]() ∠BAD 时,EF与DF、BE之间的数量关系是否发生改变?请给出详细的证明过程;
∠BAD 时,EF与DF、BE之间的数量关系是否发生改变?请给出详细的证明过程;
●拓展应用 在(3)中,若BC=4,DC=7,CF=2,求△CEF的周长.
参考答案:
【答案】●特例发现, EF=DF-BE;●深入探究 ,EF=DF-BE;EF=DF-BE,证明见解析;●拓展应用△CEF的周长为15.
【解析】试题分析:“特例发现”与” “深入探究”解题思路一致,都是通过两步全等来实现;在DC上截取DG=BE,第一步,首先证△ADG≌△ABE,得AE=AG;第二步,证△AGF≌△AEF,得EF=GF,由此得到DF、EF、BE的数量关系.
根据前三问的结论知:EF=DF-BE,那么△CEF的周长可转化为:CE+EF+FC=CE+(DF-BE)+FC =BC+DC+2FC,从而得解.
试题解析:●特例发现 EF=DF-BE;
●深入探究 EF=DF-BE,
如图4,在DC上截取DG,使DG=BE,连接AG.
∵∠D+∠ABC=180°,∠ABC+∠ABE=180°,
∴∠ABE=∠D.
又∵AB=AD,DG=BE,
∴△ABE≌△ADG(SAS).
∴∠BAE=∠DAG,AE=AG.
又∵∠DAG+∠BAF=∠BAE+∠BAF=∠EAF=![]() ∠BAD,
∠BAD,
∴∠GAF=∠BAD-(∠DAG+∠BAF)=![]() ∠BAD,
∠BAD,
∴∠GAF=∠EAF.
∵AE=AG (前面已证),AF=AF,
∴△AFE≌△AFG(SAS),
∴EF=GF.
∴EF=GF=DF-DG=DF-BE.

●拓展应用
△CEF的周长:CE+EF+FC=CE+(DF-BE)+FC
=(CE-BE)+DF+FC
=(CE-BE)+(DC+FC)+FC
=BC+DC+2FC
=4+7+2×2
=15.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图在四边形ABCD中,AB∥CD,AD=BC,AB=2,CD=
 ,∠D=30°.∠MON=60°,其顶点O在CD边上运动,并保持OM始终经过点B,设ON与AD边所在的直线交于点P,则当AP=______时,△OBC为等腰三角形.
,∠D=30°.∠MON=60°,其顶点O在CD边上运动,并保持OM始终经过点B,设ON与AD边所在的直线交于点P,则当AP=______时,△OBC为等腰三角形.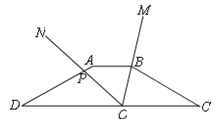
-
科目: 来源: 题型:
查看答案和解析>>【题目】六月份某登山队在山顶测得温度为零下32度,此时山脚下的温度为零上12度,则山顶的温度比山脚下的温度低( )
A.20°
B.﹣20℃
C.44℃
D.﹣44℃ -
科目: 来源: 题型:
查看答案和解析>>【题目】有9名同学参加歌咏比赛,他们的预赛成绩各不相同,现取其中前4名参加决赛,小红同学在知道自己成绩的情况下,要判断自己能否进入决赛,还需要知道这9名同学成绩的( )
A.众数
B.中位数
C.平均数
D.极差 -
科目: 来源: 题型:
查看答案和解析>>【题目】在Rt△ABC中,各边都扩大3倍,则角A的正弦值( )
A.扩大3倍B.缩小3倍C.不变D.不能确定
-
科目: 来源: 题型:
查看答案和解析>>【题目】若|a+3|+|b﹣2|=0,则ab的值为( )
A.﹣6
B.﹣9
C.9
D.6 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,折叠矩形ABCD,使点B落在对角线AC上的点F处,若BC=4,AB=3,则线段CE的长度是( )
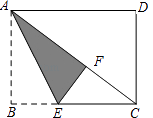
A.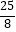
B.
C.3
D.2.8
相关试题

