【题目】在四边形ABCD(凸四边形)中, AB=AD=BC,∠BAD=90°,连结对角线 AC,当△ACD为等腰三角形时,则∠BCD的度数为
参考答案:
【答案】135°、90°、150°
【解析】解:
∵△ACD是等腰三角形.
如图1,当AD=AC时,
∵AB=AD=BC,
∴AB=AC=BC,
∴△ABC是正三角形,
∴∠ACB=∠BAC=60°,
∵∠BAD=90°,
∴∠CAC=90°-60°=30°,
∵AC=AD,
∴∠ACD= ![]() (180°-30°)=75°,
(180°-30°)=75°,
∴∠BCD=60°+75°=135°;
如图2,当AD=CD时,
∵AB=AD=BC,
∴AB=AD=BC=CD,
∵∠BAD=90°,
∴四边形ABCD是正方形,
∴∠BCD=90°;
如图3,当AC=CD时,过点C作CE⊥AD于E,过点B作BF⊥CE于F,
∵AC=CD,CE⊥AD,
∴AE= ![]() AD,∠ACE=∠DCE.
AD,∠ACE=∠DCE.
∵∠BAD=∠AEF=∠BFE=90°,
∴四边形ABFE是矩形,
∴BF=AE.
∵AB=AD=BC,
∴BF= ![]() BC,
BC,
∴∠BCF=30°.
∵AB∥CE,AB=BC,
∴∠ACF=∠BAC=∠BCA= ![]() ∠BCF=15°,
∠BCF=15°,
∴∠BCD=3∠BCA=45°.
综上所述,∠ABC的度数为135°、90°、45°.
所以答案是:135°、90°、45°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】应用题
某校为了奖励在数学竞赛中获胜的学生,买了若干本课外读物准备送给他们,如果每人送3本,则还余8本;
(1)如果前面每人送5本,则最后一人得到的课外读物只有3本;求有几名学生获奖?
(2)如果前面每人送5本,则最后一人得到了课外读物,但是不足3本,求有几名学生获奖? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,等腰三角形ABC的底边BC长为4,面积是16,腰AC的垂直平分线EF分别交AC,AB边于E,F点.若点D为BC边的中点,点M为线段EF上一动点,则△CDM周长的最小值为( )
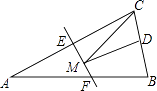
A.6
B.8
C.10
D.12 -
科目: 来源: 题型:
查看答案和解析>>【题目】完成下面证明:
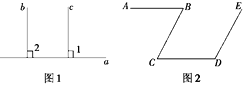
(1)如图1,已知直线b∥c,a⊥c,求证:a⊥b.
证明:∵a⊥c (已知)
∴∠1=(垂直定义)
∵b∥c (已知)
∴∠1=∠2 ()
∴∠2=∠1=90° ()
∴a⊥b ()
(2)如图2:AB∥CD,∠B+∠D=180°,求证:CB∥DE.
证明:∵AB∥CD (已知)
∴∠B=()
∵∠B+∠D=180° (已知)
∴∠C+∠D=180° ()
∴CB∥DE () -
科目: 来源: 题型:
查看答案和解析>>【题目】-2x2y(3xy2-2y2z)= ______ .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC是⊙O的内接三角形,AB为直径,过点B的切线与AC的延长线交于点D,E是BD中点,连接CE.
(1)求证:CE是⊙O的切线;
(2)若AC=4,BC=2,求BD和CE的长.
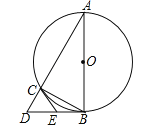
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点E、F、C、B在同一直线上,AB=DE,∠B=∠E,要判定△ABC≌△DEF,还需要添加一个条件,你添加的条件是(写出一个即可)
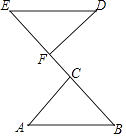
相关试题

