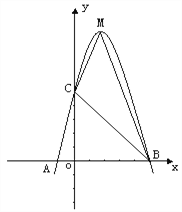
【题目】已知:如图,二次函数y=ax2+bx+c的图象与x轴交于A、B两点,其中A点坐标为(-1,0),点C(0,5),另抛物线经过点(1,8),M为它的顶点.
(1)求抛物线的解析式;
(2)求出对称轴和顶点坐标.
参考答案:
【答案】(1)抛物线的解析式为![]() ,(2)对称轴x=2, 顶点坐标 (2,9).
,(2)对称轴x=2, 顶点坐标 (2,9).
【解析】试题分析:(1)、把三点代入函数解析式列出三元一次方程组,从而得出函数解析式;(2)、根据函数解析式求出点B和点M的坐标,然后作ME⊥y轴于点E,根据△MCB的面积=梯形EDBM的面积-△ECM的面积-△COB的面积得出答案.
试题解析:(1)依题意:

(2)令y=0,得(x-5)(x+1)=0,x1=5,x2=-1 ∴B(5,0)
由![]() ,得M(2,9) 作ME⊥y轴于点E,
,得M(2,9) 作ME⊥y轴于点E,

则![]() 可得S△MCB=15.
可得S△MCB=15.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在两个命题中,如果第一个命题的题设是第二个命题的结论,而第一个命题的结论是第二个命题的题设,那么这两个命题叫做____________;如果把其中一个命题叫做原命题,那么另一个命题叫做它的____________.
-
科目: 来源: 题型:
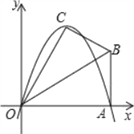
查看答案和解析>>【题目】已知在Rt△OAB中,∠OAB=90°,∠BOA=30°,AB=2.若以O为坐标原点,OA所在直线为x轴,建立如图所示的平面直角坐标系,点B在第一象限内.将Rt△OAB沿OB折叠后,点A落在第一象限内的点C处.
(1)求点C的坐标;
(2)若抛物线y=ax2+bx(a≠0)经过C、A两点,求此抛物线的解析式;
(3)若抛物线的对称轴与OB交于点D,点P为线段DB上一点,过P作y轴的平行线,交抛物线于点M.问:是否存在这样的点P,使得四边形CDPM为等腰梯形?若存在,请求出此时点P的坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】与抛物线y=2(x﹣4)2﹣1,关于x轴对称的抛物线的解析式为_____.
-
科目: 来源: 题型:
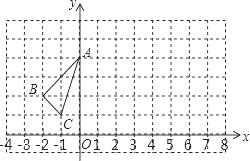
查看答案和解析>>【题目】在边长为1的小正方形网格中,△ABC的顶点均在格点上,
(1)B点关于y轴的对称点坐标为 ;
(2)将△ABC向右平移3个单位长度得到△A1B1C1,请画出△A1B1C1;
(3)在(2)的条件下,A1的坐标为 ;
(4)求△ABC的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD中有一点P,边长为4,且△PBC是等边三角形,则∠APD= , S△APB= .

相关试题

