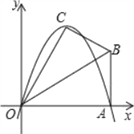
【题目】已知在Rt△OAB中,∠OAB=90°,∠BOA=30°,AB=2.若以O为坐标原点,OA所在直线为x轴,建立如图所示的平面直角坐标系,点B在第一象限内.将Rt△OAB沿OB折叠后,点A落在第一象限内的点C处.
(1)求点C的坐标;
(2)若抛物线y=ax2+bx(a≠0)经过C、A两点,求此抛物线的解析式;
(3)若抛物线的对称轴与OB交于点D,点P为线段DB上一点,过P作y轴的平行线,交抛物线于点M.问:是否存在这样的点P,使得四边形CDPM为等腰梯形?若存在,请求出此时点P的坐标;若不存在,请说明理由.
参考答案:
【答案】(1)(![]() ,3)(2)
,3)(2)![]() (3)存在,(
(3)存在,( ![]() ,
, ![]() )
)
【解析】解:(1)过C作CH⊥OA于H,
∵在Rt△OAB中,∠OAB=90°,∠BOA=30°,AB=2,∴OA=![]() 。
。
∵将Rt△OAB沿OB折叠后,点A落在第一象限内的点C处,
∴OC=OA=![]() ,∠AOC=60°。
,∠AOC=60°。
∴OH=![]() ,CH="3" 。
,CH="3" 。
∴C的坐标是(![]() ,3)。
,3)。
(2)∵抛物线![]() 经过C(
经过C(![]() ,3)、A(
,3)、A(![]() ,0)两点,
,0)两点,
∴ ,解得
,解得 。∴此抛物线的解析式为
。∴此抛物线的解析式为![]()
(3)存在。
∵![]() 的顶点坐标为(
的顶点坐标为(![]() ,3),即为点C。
,3),即为点C。
MP⊥x轴,设垂足为N,PN=t,
∵∠BOA=300,所以ON=![]()
∴P(![]() )
)
作PQ⊥CD,垂足为Q,ME⊥CD,垂足为E。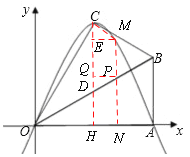
把![]() 代入
代入![]() 得:
得: ![]() 。
。
∴ M(![]() ,
, ![]() ),E(
),E(![]() ,
, ![]() )。
)。
同理:Q(![]() ,t),D(
,t),D(![]() ,1)。
,1)。
要使四边形CDPM为等腰梯形,只需CE=QD,
即![]() ,解得:
,解得: ![]() ,
, ![]() (舍去)。
(舍去)。
∴ P点坐标为(![]() ,
, ![]() )。
)。
∴ 存在满足条件的点P,使得四边形CDPM为等腰梯形,此时P点的坐为(![]() ,
, ![]() )。
)。
(1)过C作CH⊥OA于H,根据折叠得到OC=OA=4,∠A0C=60°,求出OH和CH即可。
(2)把C(![]() ,3)、A(
,3)、A(![]() ,0)代入
,0)代入![]() 得到方程组,求出方程组的解即可。
得到方程组,求出方程组的解即可。
(3)如图,根据等腰梯形的判定,只要CE=QD即可,据此列式求解。
-
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线y=2x2向右平移1个单位,再向上平移5个单位,则平移后的抛物线的解析式为( )
A.y=2(x+1)2+5
B.y=2(x+1)2﹣5
C.y=2(x﹣1)2﹣5
D.y=2(x﹣1)2+5 -
科目: 来源: 题型:
查看答案和解析>>【题目】将下列多项式因式分解,结果中不含因式x-1的是( )
A. x2-1 B. x(x-2)+(2-x) C. x2+2x+1 D. x2-2x+1
-
科目: 来源: 题型:
查看答案和解析>>【题目】在两个命题中,如果第一个命题的题设是第二个命题的结论,而第一个命题的结论是第二个命题的题设,那么这两个命题叫做____________;如果把其中一个命题叫做原命题,那么另一个命题叫做它的____________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】与抛物线y=2(x﹣4)2﹣1,关于x轴对称的抛物线的解析式为_____.
-
科目: 来源: 题型:
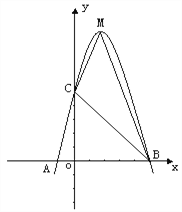
查看答案和解析>>【题目】已知:如图,二次函数y=ax2+bx+c的图象与x轴交于A、B两点,其中A点坐标为(-1,0),点C(0,5),另抛物线经过点(1,8),M为它的顶点.
(1)求抛物线的解析式;
(2)求出对称轴和顶点坐标.
-
科目: 来源: 题型:
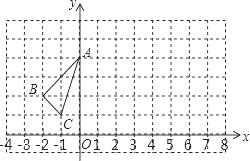
查看答案和解析>>【题目】在边长为1的小正方形网格中,△ABC的顶点均在格点上,
(1)B点关于y轴的对称点坐标为 ;
(2)将△ABC向右平移3个单位长度得到△A1B1C1,请画出△A1B1C1;
(3)在(2)的条件下,A1的坐标为 ;
(4)求△ABC的面积.
相关试题

