【题目】如图,点E是正方形ABCD内一点,△CDE是等边三角形,连接EB、EA,延长BE交边AD点于点F. 
(1)求证:△ADE≌△BCE;
(2)求∠AFB的度数.
参考答案:
【答案】
(1)证明:∵ABCD是正方形
∴AD=BC,∠ADC=∠BCD=90°
又∵三角形CDE是等边三角形
∴CE=DE,∠EDC=∠ECD=60°
∴∠ADE=∠ECB
∴△ADE≌△BCE.
(2)解:∵△CDE是等边三角形,
∴CE=CD=DE,
∵四边形ABCD是正方形
∴CD=BC,
∴CE=BC,
∴△CBE为等腰三角形,且顶角∠ECB=90°﹣60°=30°
∴∠EBC= ![]() (180°﹣30°)=75°
(180°﹣30°)=75°
∵AD∥BC
∴∠AFB=∠EBC=75°.
【解析】(1)由题意正方形ABCD的边AD=DC,在等边三角形CDE中,CE=DE,∠EDC等于∠ECD,即能证其全等.(2)根据等边三角形、等腰三角形、平行线的角度关系,可以求得∠AFB的度数.
【考点精析】根据题目的已知条件,利用正方形的性质的相关知识可以得到问题的答案,需要掌握正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,是2002年北京第24届国际数学家大会会徽,由4个全等的直角三角形拼合而成,如果大正方形的面积是13,小正方形的面积是1,直角三角形的短直角边为a,较长直角边为b,那么(a+b)2的值为( )

A.13
B.19
C.25
D.169 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD是正方形,以CD为边作等边三角形CDE,BE与AC相交于点M,则∠AMD的度数是( )

A.75°
B.60°
C.54°
D.67.5° -
科目: 来源: 题型:
查看答案和解析>>【题目】如上图所示.已知:在正方形ABCD中,∠BAC的平分线交BC于E,作EF⊥AC于F,作FG⊥AB于G.则
 = .
= . 
-
科目: 来源: 题型:
查看答案和解析>>【题目】八年级(3)班开展了手工制作竞赛,每名同学都需在规定时间内完成一件手工作品.陈莉同学在制作手工作品时的第一、二个步骤是:①如图17,先裁下一张长BC=20 cm,宽AB=16 cm 的长方形纸片ABCD;②将纸片沿着直线AE折叠,点D恰好落在BC边上的点F处.请你根据步骤①②解答下列问题:
(1)找出图中∠FEC的余角;
(2)求EC的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在进行二次根式的化简与运算时,如遇到
 ,
,  ,
,  这样的式子,还需做进一步的化简:
这样的式子,还需做进一步的化简: =
=  =
=  .①
.① =
= 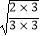 =
=  .②
.② =
=  =
=  =
=  ﹣1.③
﹣1.③
以上化简的步骤叫做分母有理化. 还可以用以下方法化简:
还可以用以下方法化简: =
=  =
=  =
=  =
=  ﹣1.④
﹣1.④
(1)请用不同的方法化简
(I)参照③式化简 =
=
(II)参照④式化简
(2)化简: +
+  +
+  +…+
+…+  .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在菱形ABCD中,∠ABC=60°,E是对角线AC上任意一点,F是线段BC延长线上一点,且CF=AE,连接BE、EF.

(1)如图1,当E是线段AC的中点,且AB=2时,求△ABC的面积;
(2)如图2,当点E不是线段AC的中点时,求证:BE=EF;
(3)如图3,当点E是线段AC延长线上的任意一点时,(2)中的结论是否成立?若成立,请给予证明;若不成立,请说明理由.
相关试题

