【题目】某水果店出售某种水果,已知该水果的进价为6元/千克,若以9元/千克的价格销售,则每天可售出200千克;若以11元/千克的价格销售,则每天可售出120千克.通过调查验证,我发现每天的销售量y(千克)与销售单价x(元)之间存在一次函数关系.
(1)求y(千克)与x(元)(x>0)的函数关系式;
(2)当销售单价为何值时,该水果店销售这种水果每天获取的利润达到280元?
(3)水果店在进货成本不超过720元时,销售单价定为多少元可获得最大利润?最大利润是多少?
参考答案:
【答案】(1)y=-40x+560;(2)13元或7元;(3)11,600
【解析】试题分析:(1)以9元/千克的价格销售,那么每天可售出200千克;以11元/千克的价格销售,那么每天可售出120千克,就相当于直线过点(9,200),(11,120),然后列方程组解答即可;
(2)根据利润=销售量×(销售单价﹣进价)写出方程求出即可;
(3)根据利润=销售量×(销售单价﹣进价)写出解析式,然后利用配方法求最大值,再结合二次函数性质得出答案.
试题解析:解:(1)设y(千克)与x(元)(x>0)的函数关系式为:y=kx+b,根据题意可得: ![]() ,解得:
,解得: ![]() .
.
故y(千克)与x(元)(x>0)的函数关系式为:y=﹣40x+560;
(2)∵W=280元,∴280=(﹣40x+560)×(x﹣6)
解得:x1=7,x2=13.
答:当销售单价为7元或13元时,每天可获得的利润达到W=280元;
(3)∵利润=销售量×(销售单价﹣进价)
∴W=(﹣40x+560)(x﹣6)
=﹣40x2+800x﹣3360
=﹣40(x﹣10)2+640
当售价为10元,则y=560﹣400=160,160×6=960(元)>720元,则当(﹣40x+560)×6=720,解得:x=11.
即当销售单价为11元时,每天可获得的利润最大,最大利润是600元.
-
科目: 来源: 题型:
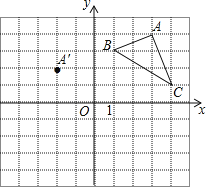
查看答案和解析>>【题目】在平面直角坐标系中,△ABC的三个顶点的位置如图所示,点A′的坐标是(﹣2,2),现将△ABC平移.使点A变换为点A′,点B′、C′分别是B、C的对应点.
(1)请画出平移后的△A′B′C′(不写画法),并直接写出点B′的坐标:B′(_____________);
(2)若△ABC内部一点P的坐标为(a,b),则点P的对应点P′的坐标是(________________);
(3)求出△ABC的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知反比例函数
 的图象的一支位于第一象限.
的图象的一支位于第一象限.(1)判断该函数图象的另一支所在的象限,并求m的取值范围;
(2)如图,O为坐标原点,点A在该反比例函数位于第一象限的图象上,点B与点A关于
 轴对称,若△OAB的面积为6,求m的值.
轴对称,若△OAB的面积为6,求m的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某区教育部门准备在七年级开设兴趣课堂,以丰富学生课余生活.为了了解学生对音乐、书法、球类、绘画这四个兴趣小组的喜爱情况,在全区进行随机抽样调查,并根据收集的数据绘制了下面两幅统计图(信息不完整),请根据图中提供的信息,解答下面的问题:
(1) 此次共调查了 名同学;
(2) 将条形图补充完整,计算扇形统计图中音乐部分的圆心角的度数是 ;
(3) 如果该区七年级共有2 000名学生参加这4个课外兴趣小组,而每名教师最多只能辅导本组的20名学生,则绘画兴趣小组至少需要准备多少名教师?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知A(-4,
 )、B(2,-4)是一次函数
)、B(2,-4)是一次函数 的图象和反比例函数
的图象和反比例函数 的图象的两个交点.
的图象的两个交点.(1)求反比例函数和一次函数的解析式;
(2)求直线AB和
 轴的交点C的坐标;
轴的交点C的坐标;(3)求方程
 的解(请直接写出答案);
的解(请直接写出答案);(4)求不等式
 的解集(请直接写出答案).
的解集(请直接写出答案).
-
科目: 来源: 题型:
查看答案和解析>>【题目】清明时节,张老师和王老师组织八年级
 班学生步行到距学校
班学生步行到距学校 千米的烈士陵园扫墓.出发时,王老师带领学生先出发,
千米的烈士陵园扫墓.出发时,王老师带领学生先出发, 分钟后,张老师骑自行车出发,张老师骑自行车的速度是学生步行速度的
分钟后,张老师骑自行车出发,张老师骑自行车的速度是学生步行速度的 倍,当学生到达烈士陵园时,张老师已经到达
倍,当学生到达烈士陵园时,张老师已经到达 个小时,并为大家买好了扫墓门票.
个小时,并为大家买好了扫墓门票. (1)求学生的步行速度和张老师骑自行车的速度各是多少;
(2)当张老师追上学生时,距离烈士陵园还有多远?
-
科目: 来源: 题型:
查看答案和解析>>【题目】综合与探究:
如图,在平面直角坐标系中,直线
 与
与 轴交于点
轴交于点 ,与直线
,与直线 交于点
交于点 , 直线
, 直线 与
与 轴交于点
轴交于点 .
.(1)求直线
 的函数表达式;
的函数表达式; (2)在线段
 上找一点
上找一点 ,使得
,使得 与
与 的面积相等,求出点
的面积相等,求出点 的坐标;
的坐标; (3)y轴上有一动点
 ,直线
,直线 上有一动点
上有一动点 ,若
,若 是以线段
是以线段 为斜边的等腰直角三角形,求出点
为斜边的等腰直角三角形,求出点 的坐标.
的坐标.
相关试题

