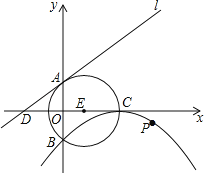
【题目】如图,⊙E的圆心E(3,0),半径为5,⊙E与y轴相交于A、B两点(点A在点B的上方),与x轴的正半轴相交于点C;直线l的解析式为y=![]() x+4,与x轴相交于点D;以C为顶点的抛物线经过点B.
x+4,与x轴相交于点D;以C为顶点的抛物线经过点B.
(1)求抛物线的解析式;
(2)判断直线l与⊙E的位置关系,并说明理由;
(3) 动点P在抛物线上,当点P到直线l的距离最小时,求出点P的坐标及最小距离.
参考答案:
【答案】(1)y=-![]() x2+x-4;(2)直线l与⊙E相切与A.(3) 抛物线上的动点P的坐标为(2,-
x2+x-4;(2)直线l与⊙E相切与A.(3) 抛物线上的动点P的坐标为(2,-![]() )时,点P到直线l的距离最小,其最小距离为
)时,点P到直线l的距离最小,其最小距离为![]() .
.
【解析】
试题分析:(1)连接AE,由已知得:AE=CE=5,OE=3,利用勾股定理求出OA的长,结合垂径定理求出OC的长,从而得到C点坐标,进而得到抛物线的解析式;
(2)求出点D的坐标为(-![]() ,0),根据△AOE∽△DOA,求出∠DAE=90°,判断出直线l与⊙E相切与A.
,0),根据△AOE∽△DOA,求出∠DAE=90°,判断出直线l与⊙E相切与A.
(3)过点P作直线l的垂线段PQ,垂足为Q,过点P作直线PM垂直于x轴,交直线l于点M.设M(m,![]() m+4),P(m,-
m+4),P(m,-![]() m2+m-4),得到PM=
m2+m-4),得到PM=![]() m+4-(-
m+4-(-![]() m2+m-4)=
m2+m-4)=![]() m2-
m2-![]() m+8=
m+8=![]() (m-2)2+
(m-2)2+![]() ,根据△PQM的三个内角固定不变,得到PQ最小=PM最小
,根据△PQM的三个内角固定不变,得到PQ最小=PM最小![]() sin∠QMP=PM最小
sin∠QMP=PM最小![]() sin∠AEO=
sin∠AEO=![]() ×
×![]() =
=![]() ,从而得到最小距离.
,从而得到最小距离.
试题解析:(1)如图1,连接AE,由已知得:AE=CE=5,OE=3,
在Rt△AOE中,由勾股定理得,OA=![]() ,
,
∵OC⊥AB,
∴由垂径定理得,OB=OA=4,
OC=OE+CE=3+5=8,
∴A(0,4),B(0,-4),C(8,0),
∵抛物线的顶点为C,
∴设抛物线的解析式为y=a(x-8)2,
将点B的坐标代入上解析的式,得64a=-4,故a=-![]() ,
,
∴y=-![]() (x-8)2,
(x-8)2,
∴y=-![]() x2+x-4为所求抛物线的解析式,
x2+x-4为所求抛物线的解析式,
(2)在直线l的解析式y=![]() x+4中,令y=0,得
x+4中,令y=0,得![]() x+4=0,解得x=-
x+4=0,解得x=-![]() ,
,
∴点D的坐标为(-![]() ,0),
,0),
当x=0时,y=4,
∴点A在直线l上,
在Rt△AOE和Rt△DOA中,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∵∠AOE=∠DOA=90°,
∴△AOE∽△DOA,
∴∠AEO=∠DAO,
∵∠AEO+∠EAO=90°,
∴∠DAO+∠EAO=90°,即∠DAE=90°,因此,直线l与⊙E相切与A.
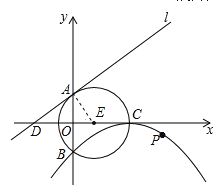
(3)如图2,过点P作直线l的垂线段PQ,垂足为Q,过点P作直线PM垂直于x轴,交直线l于点M.

设M(m,![]() m+4),P(m,-
m+4),P(m,-![]() m2+m-4),则
m2+m-4),则
PM=![]()
![]() m+4-(-
m+4-(-![]() m2+m-4)=
m2+m-4)=![]() m2-
m2-![]() m+8=
m+8=![]() (m-2)2+
(m-2)2+![]() ,
,
当m=2时,PM取得最小值![]() ,
,
此时,P(2,-![]() ),
),
对于△PQM,
∵PM⊥x轴,
∴∠QMP=∠DAO=∠AEO,
又∠PQM=90°,
∴△PQM的三个内角固定不变,
∴在动点P运动的过程中,△PQM的三边的比例关系不变,
∴当PM取得最小值时,PQ也取得最小值,
PQ最小=PM最小![]() sin∠QMP=PM最小
sin∠QMP=PM最小![]() sin∠AEO=
sin∠AEO=![]() ×
×![]() =
=![]() ,
,
∴当抛物线上的动点P的坐标为(2,-![]() )时,点P到直线l的距离最小,其最小距离为
)时,点P到直线l的距离最小,其最小距离为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算正确的是
A. a5+a5=a10 B. a3·a3=a9 C. (3a3)3=9a9 D. a12÷a3=a9
-
科目: 来源: 题型:
查看答案和解析>>【题目】一次选拔考试的及格率为25%,及格者的平均分数比规定的及格分数多15分,不及格者的平均分数比规定的及格分数少25分,又知全体考生的平均分数是60分,求这次考试规定的及格分数是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD中,O为AC中点,过点O的直线分别与AB,CD交于点E,F,连接BF交AC于点M,连接DE,BO.若∠COB=60°,FO=FC,则下列结论:①FB⊥OC,OM=CM;②△EOB≌△CMB;③四边形EBFD是菱形;④MB:OE=3:2.其中正确结论的个数是 ( )

A.1 B.2 C.3 D.4
-
科目: 来源: 题型:
查看答案和解析>>【题目】己知拋物线y=x2﹣2x﹣3,当﹣2≤x≤0时,y的取值范围是____________
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB=AD,那么添加下列一个条件后,仍无法判定△ABC≌△ADC的是( )
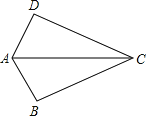
A.CB=CD
B.∠BAC=∠DAC
C.∠BCA=∠DCA
D.∠B=∠D=90°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点P是∠AOB的角平分线OC上一点,分别连接AP、BP,若再添加一个条件即可判定△AOP≌△BPO,则一下条件中:①∠A=∠B;②∠APO=∠BPO;③∠APC=∠BPC; ④AP=BP;⑤OA=OB.其中一定正确的是 (只需填序号即可)

相关试题

