【题目】定义一种新运算“⊕”:a⊕b=2a﹣ab,比如1⊕(﹣3)=2×1﹣1×(﹣3)=5
(1)求(﹣2)⊕3的值;
(2)若(﹣3)⊕x=(x+1)⊕5,求x的值;
(3)若x⊕1=2(1⊕y),求代数式![]() x+y+1的值.
x+y+1的值.
参考答案:
【答案】(1)2;(2)![]() ;(3)3.
;(3)3.
【解析】
(1)根据一种新运算“⊕”:a⊕b=2a﹣ab的定义求解即可;
(2)根据一种新运算“⊕”:a⊕b=2a﹣ab的定义求解即可;
(3)根据一种新运算的定义求出x,y的值,再代入代数式求解即可.
解:(1)∵a⊕b=2a﹣ab,
∴(﹣2)⊕3=2×(﹣2)﹣(﹣2)×3=2,
(2)由题意知,(﹣3)⊕x=2×(﹣3)﹣(﹣3)x=3x﹣6
(x+1)⊕5=2(x+1)﹣5(x+1)=﹣3x﹣3,
∵(﹣3)⊕x=(x+1)⊕5,
∴3x﹣6=﹣3x﹣3,
∴x=![]() ,
,
(3)由题意知,x⊕1=2x﹣x=x,2(1⊕y)=2(2×1﹣y)=﹣2y+4,
∵x⊕1=2(1⊕y),
∴x=﹣2y+4,
∴x+2y=4,
∴![]() x+y=2,
x+y=2,
∴![]() x+y+1=2+1=3.
x+y+1=2+1=3.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠B=90°,AC=60cm,∠A=60°,点D从点C出发沿CA方向以4cm/秒的速度向点A匀速运动,同时点E从点A出发沿AB方向以2cm/秒的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是t秒(0<t≤15).过点D作DF⊥BC于点F,连接DE,EF.

(1)求证:AE=DF;
(2)四边形AEFD能够成为菱形吗?如果能,求出相应的t值,如果不能,说明理由;
(3)当t为何值时,△DEF为直角三角形?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我市为创建“国家园林城市”,某校举行了以“爱我冷江”为主题的图片制作比赛,评委会对200名同学的参赛作品打分发现,参赛者的成绩x均满足50≤x<100,并制作了频数分布直方图,如图:

根据以上信息,解答下列问题:
(1)请补全频数分布直方图;
(2)若依据成绩,采取分层抽样的方法,从参赛同学中抽40人参加图片制作比赛总结大会,则从成绩80≤x<90的选手中应抽多少人?
(3)比赛共设一、二、三等奖,若只有25%的参赛同学能拿到一等奖,则一等奖的分数线是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知正方形ABCD的边长为24厘米.甲、乙两动点同时从顶点A出发,甲以2厘米/秒的速度沿正方形的边按顺时针方向移动,乙以4厘米/秒的速度沿正方形的边按逆时针方向移动,每次相遇后甲乙的速度均增加1厘米/秒且都改变原方向移动,则第四次相遇时甲与最近顶点的距离是______厘米.

-
科目: 来源: 题型:
查看答案和解析>>【题目】若顺次连接四边形的各边中点所得的四边形是菱形,则该四边形一定是( )
A. 矩形 B. 一组对边相等,另一组对边平行的四边形
C. 对角线互相垂直的四边形 D. 对角线相等的四边形
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等腰△ABC中,AB=AC=5,BC=6,AD⊥BC于点D,动点P从点B出发沿BC方向以每秒5个单位的速度向终点C运动,过点P作PE⊥AB于点E,过点P作PF∥BA,交AC于点F,设点P运动的时间为t秒.若以PE所在的直线为对称轴,线段BD经轴对称变换后的图形为B'D',求当线段B'D'与线段AC有交点这段过程中,线段B'D'扫过的面积 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】一组数据x1,x2,x3,x4,x5的平均数是a,另一组数据
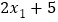 ,
,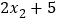 ,
,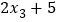 ,
,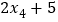 ,
,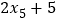 的平均数是( )
的平均数是( )A. a B. 2a C. 2a+5 D. 无法确定
相关试题

