【题目】如图,在等腰△ABC中,AB=AC=5,BC=6,AD⊥BC于点D,动点P从点B出发沿BC方向以每秒5个单位的速度向终点C运动,过点P作PE⊥AB于点E,过点P作PF∥BA,交AC于点F,设点P运动的时间为t秒.若以PE所在的直线为对称轴,线段BD经轴对称变换后的图形为B'D',求当线段B'D'与线段AC有交点这段过程中,线段B'D'扫过的面积 . 
参考答案:
【答案】![]()
【解析】解:由题意点B′在射线BA上,D′在过D垂直PF的直线上,
易知当线段B'D'与线段AC有交点这段过程中,线段B'D'扫过的图形是图中平行四边形AD′D″B″.
作D′M⊥AB于M,DN⊥AB于N,
在等腰梯形ABDD′中,易知四边形MNDD′是矩形,BN=AM= ![]() ,MN=DD′=5﹣
,MN=DD′=5﹣ ![]() =
= ![]() ,DN=
,DN= ![]() ,
,
∵BD=DC,DD″∥AB,
∴AD″=D″C,
在Rt△ADC中,DD″= ![]() AC=
AC= ![]() ,
,
∴D′D″=DD″﹣DD′= ![]() ﹣
﹣ ![]() =
= ![]() ,
,
∴当线段B'D'与线段AC有交点这段过程中,线段B'D'扫过的面积= ![]() ×
× ![]() =
= ![]() ,
,
所以答案是 ![]() .
.
【考点精析】解答此题的关键在于理解等腰三角形的性质的相关知识,掌握等腰三角形的两个底角相等(简称:等边对等角).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知正方形ABCD的边长为24厘米.甲、乙两动点同时从顶点A出发,甲以2厘米/秒的速度沿正方形的边按顺时针方向移动,乙以4厘米/秒的速度沿正方形的边按逆时针方向移动,每次相遇后甲乙的速度均增加1厘米/秒且都改变原方向移动,则第四次相遇时甲与最近顶点的距离是______厘米.

-
科目: 来源: 题型:
查看答案和解析>>【题目】定义一种新运算“⊕”:a⊕b=2a﹣ab,比如1⊕(﹣3)=2×1﹣1×(﹣3)=5
(1)求(﹣2)⊕3的值;
(2)若(﹣3)⊕x=(x+1)⊕5,求x的值;
(3)若x⊕1=2(1⊕y),求代数式
 x+y+1的值.
x+y+1的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】若顺次连接四边形的各边中点所得的四边形是菱形,则该四边形一定是( )
A. 矩形 B. 一组对边相等,另一组对边平行的四边形
C. 对角线互相垂直的四边形 D. 对角线相等的四边形
-
科目: 来源: 题型:
查看答案和解析>>【题目】一组数据x1,x2,x3,x4,x5的平均数是a,另一组数据
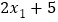 ,
,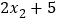 ,
,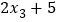 ,
,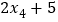 ,
,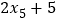 的平均数是( )
的平均数是( )A. a B. 2a C. 2a+5 D. 无法确定
-
科目: 来源: 题型:
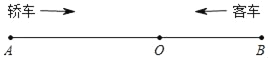
查看答案和解析>>【题目】如图,A,B两地相距450千米,两地之间有一个加油站O,且AO=270千米,一辆轿车从A地出发,以每小时90千米的速度开往B地,一辆客车从B地出发,以每小时60千米的速度开往A地,两车同时出发,设出发时间为t小时.
(1)经过几小时两车相遇?
(2)当出发2小时时,轿车和客车分别距离加油站O多远?
(3)经过几小时,两车相距50千米?
-
科目: 来源: 题型:
查看答案和解析>>【题目】综合题。
(1)计算:(π﹣3.14)0+( )﹣1+|﹣2
)﹣1+|﹣2 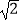 |﹣
|﹣ 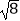 .
.
(2)先化简,再求值: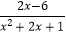 ÷(
÷( 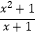 ﹣x+1),并从﹣tan60°≤x≤2cos30°取出一个合适的整数,求出式子的值.
﹣x+1),并从﹣tan60°≤x≤2cos30°取出一个合适的整数,求出式子的值.
相关试题

