【题目】春节期间,为了满足百姓的消费需求,某商场计划购进冰箱、彩电进行销售.冰箱、彩电的进价、售价如表:
进价(元/台) | 售价(元/台) | |
冰箱 | M | 2500 |
彩电 | m﹣400 | 2000 |
(1)商场用80000元购进冰箱的数量用64000元购进彩电的数量相等,求表中m的值;
(2)为了满足市场需要要求,商场决定用不超过9万元采购冰箱、彩电共50台,且冰箱的数量不少于彩电数量的![]() ;若该商场将购进的冰箱、彩电全部售出,求能获得的最大利润w的值.
;若该商场将购进的冰箱、彩电全部售出,求能获得的最大利润w的值.
参考答案:
【答案】(1)m=2000;
(2)w的最大值为22500元.
【解析】
试题分析:(1)根据总价÷单价=数量由80000元购进冰箱的数量与用64000元购进彩电的数量相等建立方程求出其解即可;
(2)设购买彩电x台,则购进冰箱(50﹣x)台.用含x的代数式表示利润W,根据x的取值范围和一次函数的性质求解.
试题解析:(1)由题意,得![]() =
=![]() ,解得:m=2000,
,解得:m=2000,
经检验,m=2000是原方程的解,且符合题意.∴m=2000;
(2)设购买冰箱x台,则购买彩电(50﹣x)台,由题意,得
W=(2500﹣2000)x+(2000﹣1600)(50﹣x),
=100x+20000.
∵k=100>0,
∴W随x的增大而增大,
∴x=25时,W最大=22500,
∴w的最大值为22500元.
-
科目: 来源: 题型:
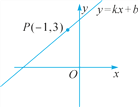
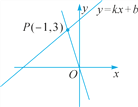
查看答案和解析>>【题目】如图,直线y=kx+b上有一点P(-1,3),回答下列问题:
(1)关于x的方程kx+b=3的解是_______.
(2)关于x的不等式kx+b>3的解是________.
(3)关于x的不等式kx+b-3<0的解是______.
(4)求不等式-3x≥kx+b的解.
(5)求不等式(k+3)x+b>0的解.
-
科目: 来源: 题型:
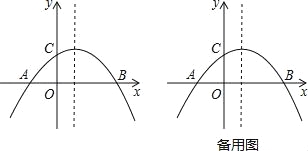
查看答案和解析>>【题目】如图,已知抛物线y=ax2+bx+c与x轴相交于A(﹣2,0),B(4,0),与y轴相交于点C,且抛物线经过点(2,2).
(1)求此抛物线的解析式;
(2)在抛物线的对称轴上找一点H,使AH+CH最小,并求出点H的坐标;
(3)在第四象限内,抛物线上是否存在点M,是的以点A、B、M为顶点的三角形与△ABC相似?若存在,请求出点M的坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】据统计,2017年春节黄金周7天,杭州共接待中外游客约450万人次,将450万用科学记数法表示,以下表示正确的是( )
A.450×104
B.45.0×105
C.4.50×106
D.4.50×107 -
科目: 来源: 题型:
查看答案和解析>>【题目】一个三位数,三个数位上的数字之和是16,百位数字比十位数字小1,个位数字比十位数字大2,则十位数字是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若x<0,则|x-(-x)|等于( )
A.-x
B.0
C.2x
D.-2x -
科目: 来源: 题型:
查看答案和解析>>【题目】在一次蜡烛实验中,甲、乙两根蜡烛燃烧时剩余部分的高度
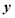 (cm)与燃烧时间
(cm)与燃烧时间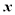 (h)的关系如图所示. 请根据图像所提供的信息解答下列各问题:
(h)的关系如图所示. 请根据图像所提供的信息解答下列各问题:
(1)甲乙两根蜡烛燃烧前的高度分别是 ,从点燃到燃尽所用的时间分别是 ;
(2)分别求出甲、乙两根蜡烛燃烧时
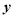 与
与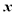 之间的函数关系式;
之间的函数关系式;(3)当
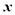 为何值时,甲、乙两根蜡烛在燃烧的过程中的高度相等?
为何值时,甲、乙两根蜡烛在燃烧的过程中的高度相等?
相关试题

