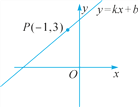
【题目】如图,直线y=kx+b上有一点P(-1,3),回答下列问题:
(1)关于x的方程kx+b=3的解是_______.
(2)关于x的不等式kx+b>3的解是________.
(3)关于x的不等式kx+b-3<0的解是______.
(4)求不等式-3x≥kx+b的解.
(5)求不等式(k+3)x+b>0的解.
参考答案:
【答案】(1)x=-1;(2)x>-1;(3)x<-1;(4)x≤-1;(5)x>-1.
【解析】试题分析:(1)利用一次函数图像性质与一元一次方程的关系.(2)(3)(4)
(5)利用一次函数图像性质与一元一次不等式的关系
试题解析:(1)因为P(-1,3)在一次函数y=kx+b图像上,所以kx+b=3得解为x=-1.
(2) 不等式kx+b>3,恰好是一次函数y=kx+b函数值大于3的部分,对应的x>-1.
(3)因为 kx+b-3<0所以kx+b<3, 恰好是一次函数y=kx+b函数值大小于3的部分对应的x<-1.
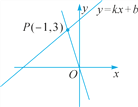
(4)观察图象可知,点(-1,3)在函数y=-3x上,构造函数y=-3x如解图.y=-3x比y=kx+b图像“高”的部分,
∴不等式-3x≥kx+b的解为x≤-1.
(5)不等式(k+3)x+b>0可变形为kx+b>-3x,仿照(4)可得x>-1.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某次数学测验共20道题,规则是:选对一道得5分,选错一道得﹣1分,不选得0分,王明同学得卷面成绩时:选对16道题,选错2道题,他的得分是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列结论不正确的是( )
A.若a<0,b>0,则a-b<0
B.若a>0,b<0,则a-b>0
C.若a<0,b<0,则a-(-b)>0
D.若a<0,b<0,且|a|>|b|,则a-b<0 -
科目: 来源: 题型:
查看答案和解析>>【题目】若a=(﹣2013)0 , b=(﹣0.5)﹣1 , c=(﹣
 )﹣2 , 则a、b、c的大小为( )
)﹣2 , 则a、b、c的大小为( )
A.a>c>b
B.c>b>a
C.c>a>b
D.a>b>c -
科目: 来源: 题型:
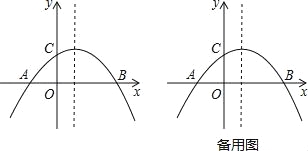
查看答案和解析>>【题目】如图,已知抛物线y=ax2+bx+c与x轴相交于A(﹣2,0),B(4,0),与y轴相交于点C,且抛物线经过点(2,2).
(1)求此抛物线的解析式;
(2)在抛物线的对称轴上找一点H,使AH+CH最小,并求出点H的坐标;
(3)在第四象限内,抛物线上是否存在点M,是的以点A、B、M为顶点的三角形与△ABC相似?若存在,请求出点M的坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】据统计,2017年春节黄金周7天,杭州共接待中外游客约450万人次,将450万用科学记数法表示,以下表示正确的是( )
A.450×104
B.45.0×105
C.4.50×106
D.4.50×107 -
科目: 来源: 题型:
查看答案和解析>>【题目】春节期间,为了满足百姓的消费需求,某商场计划购进冰箱、彩电进行销售.冰箱、彩电的进价、售价如表:
进价(元/台)
售价(元/台)
冰箱
M
2500
彩电
m﹣400
2000
(1)商场用80000元购进冰箱的数量用64000元购进彩电的数量相等,求表中m的值;
(2)为了满足市场需要要求,商场决定用不超过9万元采购冰箱、彩电共50台,且冰箱的数量不少于彩电数量的
 ;若该商场将购进的冰箱、彩电全部售出,求能获得的最大利润w的值.
;若该商场将购进的冰箱、彩电全部售出,求能获得的最大利润w的值.
相关试题

