【题目】在边长为5的正方形ABCD中,点E,F分别是BC,DC边上的两个动点(不与点B,C,D重合),且AE⊥EF.
(1)如图1,当BE=2时,求FC的长;
(2)延长EF交正方形ABCD外角平分线CP于点P.
①依题意将图2补全;
②小京通过观察、实验提出猜想:在点E运动的过程中,始终有AE=PE.小京把这个猜想与同学们进行交流,通过讨论,形成了证明该猜想的三种想法:
想法1:在AB上截取AG=EC,连接EG,要证AE=PE,需证△AGE≌△ECP.
想法2:作点A关于BC的对称点H,连接BH,CH,EH.要证AE=PE,需证△EHP为等腰三角形.
想法3:将线段BE绕点B顺时针旋转90°,得到线段BM,连接CM,EM,要证AE=PE,需证四边形MCPE为平行四边形.
请你参考上面的想法,帮助小京证明AE=PE.(一种方法即可)
参考答案:
【答案】
(1)
解∵正方形ABCD的边长为5,BE=2,
∴EC=3.
∵四边形ABCD是正方形,
∴∠B=∠C=90°,
∴∠BAE+∠AEB=90°,
∵AE⊥EF,
∴∠FEC+∠AEB=90°,
∴∠BAE=∠CEF.
∴△ABE∽△ECF,
∴ ![]() ,即
,即 ![]() ,
,
∴FC= ![]()
(2)
解:①依题意补全图形:
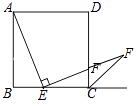
②证明:在AB上截取AG=EC,连接EG.
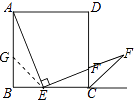
∵AB=BC,
∴GB=EB.
∵∠B=90°,
∴∠BGE=45°,
∴∠AGE=135°.
∵∠DCB=90°,CP是正方形ABCD外角平分线,
∴∠ECP=135°.
∴∠AGE=∠ECP.
在△AGE和△ECP中,
 ,
,
∴△AGE≌△ECP.
∴AE=PE.
【解析】(1)根据正方形的性质求出EC,证明△ABE∽△ECF,根据相似三角形的性质列出比例式,计算即可;(2)①根据题意画图;②在AB上截取AG=EC,连接EG,证明△AGE≌△ECP,根据全等三角形的性质证明.
【考点精析】通过灵活运用全等三角形的性质和相似三角形的性质,掌握全等三角形的对应边相等; 全等三角形的对应角相等;对应角相等,对应边成比例的两个三角形叫做相似三角形即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某学校组织340名师生进行长途考察活动,带有行李170件,计划租用甲、乙两种型号的汽车共10辆.经了解,甲车每辆最多能载40人和16件行李,乙车每辆最多能载30人和20件行李.
(1)请你帮助学校设计所有可行的租车方案.
(2)如果甲车的租金为每辆2 000元,乙车的租金为每辆1 800元,问哪种可行方案使租车费用最省?
-
科目: 来源: 题型:
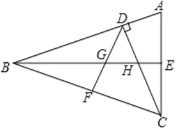
查看答案和解析>>【题目】如图,CD 和 BE 是△ABC 的两条高,∠BCD=45°,BF=FC,BE与 DF、DC分别交于点 G、H,∠ACD=∠CBE.
(1)证明:AB=BC;
(2)判断 BH 与 AE 之间的数量关系,并证明你的结论;
(3)结合已知条件,观察图形,你还能发现什么结论?请写出两个(不与前面结论相同).
-
科目: 来源: 题型:
查看答案和解析>>【题目】观察下列等式:
 ……
……(1)请写出第4个等式:________________;
(2)观察上述等式的规律,猜想第n个等式(用含n的式子表示),并验证其正确性.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC 中,∠BAC=90°,AB=AC,D 是 AC 边上一动点, CE⊥BD 于 E.
(1)如图(1),若 BD 平分∠ABC 时,①求∠ECD 的度数;②求证:BD=2EC;
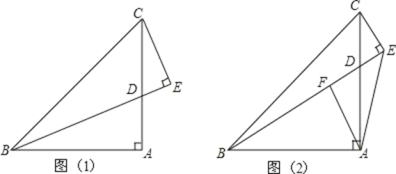
(2)如图(2),过点 A 作 AF⊥BE 于点 F,猜想线段 BE,CE,AF 之间的数量关系并证明你的猜想.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,A(0,a)、B(b,0)、C(c,0),且
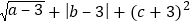 =0.
=0.(1)直接写出 A、B、C 各点的坐标:A_______;B__________;C_____;
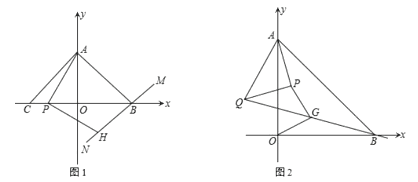
(2)过 B 作直线 MN⊥AB,P 为线段 OC 上的一动点,AP⊥PH 交直线 MN 于点 H,证明:PA=PH.
(3)在(1)的条件下,若在点 A 处有一个等腰 Rt△APQ 绕点 A 旋转,且 AP=PQ,∠APQ=90°,连接 BQ,点 G 为 BQ 的中点,试猜想线段 OG 与线段 PG 的数量关系与位置关系,并证明你的结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我们用
 表示不大于
表示不大于 的最大整数,例如:
的最大整数,例如: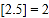 ,
,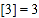 ,
, ;用
;用 表示大于
表示大于 的最小整数,例如:
的最小整数,例如: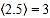 ,
, ,
, .解决下列问题:
.解决下列问题:(1)
 = ,,
= ,, = ;
= ;(2)若
 =2,则
=2,则 的取值范围是 ;若
的取值范围是 ;若 =-1,则
=-1,则 的取值范围是 ;
的取值范围是 ;(3)已知
 ,
, 满足方程组
满足方程组 ,求
,求 ,
, 的取值范围.
的取值范围.
相关试题

