【题目】如图①,在锐角△ABC中,D,E分别为AB,BC中点,F为AC上一点,且∠AFE=∠A,DM∥EF交AC于点M.
(1)求证:DM=DA;
(2)如图②,点G在BE上,且∠BDG=∠C.求证:△DEG∽△ECF;
(3)在(2)的条件下,已知EF=2,CE=3,求GE的长.
参考答案:
【答案】
(1)证明:∵DM∥EF,
∴∠AMD=∠AFE,
∵∠AFE=∠A,
∴∠AMD=∠A,
∴DM=DA;
(2)证明:∵D、E分别是AB、BC的中点,
∴DE∥AC,
∴∠BDE=∠A,∠DEB=∠C,
∴∠BDE=∠AFE,
∴∠BDG+∠GDE=∠C+∠FEC,
∵∠BDG=∠C,
∴∠GDE=∠FEC,又∠DEB=∠C,
∴△DEG∽△ECF;
(3)解:∵∠BDG=∠C=∠DEB,∠B=∠B,
∴△BDG∽△BED,
∴ ![]() ,即BD2=BEBG,
,即BD2=BEBG,
∵DE∥AC,DM∥EF,
∴四边形DEFM是平行四边形,
∴EF=DM,
又∵DM=AD,AD=BD,
∴EF=BD=2,
∵BE=CE,EF=2,CE=3,
∴22=3BG,
∴BG= ![]() ,
,
∴GE=3﹣ ![]() =
= ![]() .
.
【解析】(1)(1)根据DM∥EF得到∠AMD=∠AFE,等量代换得到∠AMD=∠A,根据等角对等边证明即可。
(2)根据三角形中位线定理得到DE∥AC,证得∠BDE=∠AFE,再根据∠BDG+∠GDE=∠C+∠FEC,证明∠GDE=∠FEC,根据相似三角形的判定定理证明。
(3)根据已知易证△BDG∽△BED,得到BD2=BEBG,再证明四边形DEFM是平行四边形,从而求出BD、BE的长,即可求得BG的长,继而得出GE的长。
【考点精析】本题主要考查了平行线的性质和三角形中位线定理的相关知识点,需要掌握两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补;连接三角形两边中点的线段叫做三角形的中位线;三角形中位线定理:三角形的中位线平行于三角形的第三边,且等于第三边的一半才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:用2辆A型车和1辆B型车装满货物一次可运货10吨;用1辆A型车和2辆B型车装满货物一次可运货11吨.某物流公司现有31吨货物,计划同时租用A型车
 辆,B型车
辆,B型车 辆,一次运完,且恰好每辆车都装满货物. 根据以上信息,解答下列问题:
辆,一次运完,且恰好每辆车都装满货物. 根据以上信息,解答下列问题:(1)1辆A型车和1辆B型车都装满货物一次可分别运货多少吨?
(2)请你帮该物流公司设计租车方案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等边△ABC中,AB=2,N为AB上一点,且AN=1,AD=
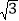 ,∠BAC的平分线交BC于点D,M是AD上的动点,连接BM、MN,则BM+MN的最小值是( )
,∠BAC的平分线交BC于点D,M是AD上的动点,连接BM、MN,则BM+MN的最小值是( )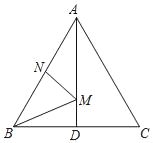
A.
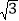 B. 2C. 1D. 3
B. 2C. 1D. 3 -
科目: 来源: 题型:
查看答案和解析>>【题目】从2017年起,昆明将迎来“高铁时代”,这就意味着今后昆明的市民外出旅行的路程与时间将大大缩短,但也有不少游客根据自己的喜好依然选择乘坐普通列车;已知从昆明到某市的高铁行驶路程是400千米,普通列车的行驶路程是高铁行驶路程的1.3倍,请完成以下问题:(1)普通列车的行驶路程为________千米;(2)若高铁的平均速度(千米/时)是普通列车平均速度(千米/时)的2.5倍,且乘坐高铁所需时间比乘坐普通列车所需时间缩短3小时,求普通列车和高铁的平均速度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】观察下列式子的因式分解做法:
①x2-1=(x-1)(x+1);
②x3﹣1
=x3﹣x+x﹣1
=x(x2﹣1)+x﹣1
=x(x﹣1)(x+1)+(x﹣1)
=(x﹣1)[x(x+1)+1]
=(x﹣1)(x2+x+1);
③x4﹣1
=x4﹣x+x﹣1
=x(x3﹣1)+x﹣1
=x(x﹣1)(x2+x+1)+(x﹣1)
=(x﹣1)[x(x2+x+1)+1]
=(x﹣1)(x3+x2+x+1);
…
(1)模仿以上做法,尝试对x5﹣1进行因式分解;
(2)观察以上结果,猜想xn﹣1= ;(n为正整数,直接写结果,不用验证)
(3)根据以上结论,试求45+44+43+42+4+1的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平面直角坐标系中,点A、B分别在x、y轴上,点B的坐标为(0,1),∠BAO=30°.
(1)求AB的长度;
(2)以AB为一边作等边△ABE,作OA的垂直平分线MN交AB的垂线AD于点D.求证:BD=OE;
(3)在(2)的条件下,连接DE交AB于F.求证:F为DE的中点.



-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,方格纸中每个小方格都是边长为1个单位长度的正方形,在建立平面直角坐标系后,⊿ABC的顶点在格点上。 且A(1,-4),B(5,-4),C(4,-1)
【1】画出⊿ABC;
【1】求出⊿ABC 的面积;

【1】若把⊿ABC向上平移2个单位长度,再向左平移4个单位长度得到⊿

 B
B C
C ,在图中画出⊿
,在图中画出⊿
 B
B C
C ,并写出B
,并写出B 的坐标。
的坐标。
相关试题

