【题目】如图,在正方形OABC中,点B的坐标是(4,4),点E、F分别在边BC、BA上,OE=2 ![]() .若∠EOF=45°,则F点的纵坐标是( )
.若∠EOF=45°,则F点的纵坐标是( ) 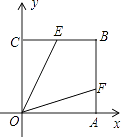
A.![]()
B.1
C.![]()
D.![]() ﹣1
﹣1
参考答案:
【答案】A
【解析】解:如图连接EF,延长BA使得AM=CE,则△OCE≌△OAM. 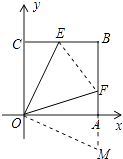
∴OE=OM,∠COE=∠MOA,
∵∠EOF=45°,
∴∠COE+∠AOF=45°,
∴∠MOA+∠AOF=45°,
∴∠EOF=∠MOF,
在△OFE和△OFM中,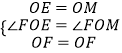 ,
,
∴△OFE≌△FOM,
∴EF=FM=AF+AM=AF+CE,设AF=x,
∵CE= ![]() =
= ![]() =2,
=2,
∴EF=2+x,EB=2,FB=4﹣x,
∴(2+x)2=22+(4﹣x)2 ,
∴x= ![]() ,
,
∴点F的纵坐标为 ![]() ,
,
故选A.
【考点精析】根据题目的已知条件,利用正方形的性质的相关知识可以得到问题的答案,需要掌握正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计如下表:
最高气温(℃)
25
26
27
28
天 数
1
1
2
3
则这组数据的中位数与众数分别是( )
A.27,28B.27.5,28C.28,27D.26.5,27
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△OAC和△BAD都是等腰直角三角形,∠ACO=∠ADB=90°,反比例函数y=
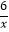 在第一象限的图象经过点B,则△OAC与△BAD的面积之差S△OAC﹣S△BAD为( )
在第一象限的图象经过点B,则△OAC与△BAD的面积之差S△OAC﹣S△BAD为( ) 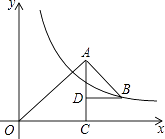
A.36
B.12
C.6
D.3 -
科目: 来源: 题型:
查看答案和解析>>【题目】用正方形硬纸板做三棱柱盒子,每个盒子由3个长方形侧面和2个等边三角形底面组成,硬纸板用如图两种方法裁剪(裁剪后边角料不再利用).

现有19张硬纸板,其中x张硬纸板用方法一裁剪,其余硬纸板用方法二裁剪.
(1)分别求裁剪出的侧面和底面的个数.(用含x的代数式表示)
(2)若裁剪出的侧面和底面恰好全部用完,问能做多少个盒子?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在坐标系中放置一菱形OABC,已知∠ABC=60°,OA=1.先将菱形OABC沿x轴的正方向无滑动翻转,每次翻转60°,连续翻转2015次,点B的落点依次为B1 , B2 , B3 , …,则B2015的坐标为 .
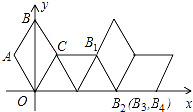
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算正确的是( )
A.a2a3=a6
B.(﹣a2)3=﹣a6
C.(ab)2=ab2
D.a6÷a3=a2 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图是函数y=
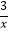 与函数y=
与函数y= 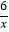 在第一象限内的图象,点P是y=
在第一象限内的图象,点P是y= 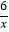 的图象上一动点,PA⊥x轴于点A,交y=
的图象上一动点,PA⊥x轴于点A,交y= 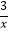 的图象于点C,PB⊥y轴于点B,交y=
的图象于点C,PB⊥y轴于点B,交y= 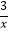 的图象于点D.
的图象于点D. 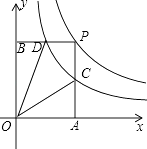
(1)求证:D是BP的中点;
(2)求四边形ODPC的面积.
相关试题

