【题目】如图, ![]() 分别平分
分别平分![]() 的外角
的外角![]() 、内角
、内角![]() 、外角
、外角![]() .以下结论: ①
.以下结论: ①![]() ;②
;②![]() ;③
;③![]() 平分
平分![]() ;④
;④![]() ; ⑤
; ⑤![]() 其中正确的结论是_______.
其中正确的结论是_______.

参考答案:
【答案】①②④⑤
【解析】试题分析:(1)由AD平分△ABC的外角∠EAC,求出∠EAD=∠DAC,由三角形外角得∠EAC=∠ACB+∠ABC,且∠ABC=∠ACB,得出∠EAD=∠ABC,利用同位角相等两直线平行得出结论正确;(2)由AD∥BC,得出∠ADB=∠DBC,再由BD平分∠ABC,所以∠ABD=∠DBC,∠ABC=2∠ADB,得出结论∠ACB=2∠ADB;(3)如果BD平分∠ADC,则四边形ABCD是菱形,只有在△ABC是正三角形时才有BD平分∠ADC故③错误;(4)在△ADC中,∠ADC+∠CAD+∠ACD=180°,利用角的关系得∠ADC+∠CAD+∠ACD=∠ADC+2∠ABD+∠ADC=2∠ADC+2∠ABD=180°,得出结论∠ADC=90°-∠ABD;(5))由∠BAC+∠ABC=∠ACF,得出![]() ∠BAC+
∠BAC+![]() ∠ABC=
∠ABC=![]() ∠ACF,再与∠BDC+∠DBC=
∠ACF,再与∠BDC+∠DBC=![]() ∠ACF相结合,得出
∠ACF相结合,得出![]() ∠BAC=∠BDC,即∠BDC=
∠BAC=∠BDC,即∠BDC=![]() ∠BAC.
∠BAC.
试题解析: (1)∵AD平分△ABC的外角∠EAC
∴∠EAD=∠DAC,
∵∠EAC=∠ACB+∠ABC,且∠ABC=∠ACB,
∴∠EAD=∠ABC,
∴AD∥BC,
故①正确。
(2)由(1)可知AD∥BC
∴∠ADB=∠DBC,
∵BD平分∠ABC,
∴∠ABD=∠DBC,
∴∠ABC=2∠ADB,
∵∠ABC=∠ACB,
∴∠ACB=2∠ADB,
故②正确;
(3) 如果BD平分∠ADC,则四边形ABCD是平行四边形,
∵∠ABD=∠ADB,
∴AB=AD,
∴四边形ABCD是菱形,
∴只有在△ABC是正三角形时才有BD平分∠ADC
故③错误;
(4) 在△ADC中,∠ADC+∠CAD+∠ACD=180°,
∵CD平分△ABC的外角∠ACF,
∴∠ACD=∠DCF,
∵AD∥BC,
∴∠ADC=∠DCF,∠ADB=∠DBC,∠CAD=∠ACB
∴∠ACD=∠ADC,∠CAD=∠ACB=∠ABC=2∠ABD,
∴∠ADC+∠CAD+∠ACD=∠ADC+2∠ABD+∠ADC=2∠ADC+2∠ABD=180°
∴∠ADC+∠ABD=90°
∴∠ADC=90°∠ABD,
故④正确;
(5)∵∠BAC+∠ABC=∠ACF,
∴![]() ∠BAC+
∠BAC+![]() ∠ABC=
∠ABC=![]() ∠ACF,
∠ACF,
∵∠BDC+∠DBC=![]() ∠ACF,
∠ACF,
∴![]() ∠BAC+
∠BAC+![]() ∠ABC=∠BDC+∠DBC,
∠ABC=∠BDC+∠DBC,
∵∠DBC=![]() ∠ABC,
∠ABC,
∴![]() ∠BAC=∠BDC,即∠BDC=img src="http://thumb.zyjl.cn/questionBank/Upload/2017/12/28/23/3361039e/SYS201712282320308096520713_DA/SYS201712282320308096520713_DA.015.png" width="16" height="41" style="-aw-left-pos:0pt; -aw-rel-hpos:column; -aw-rel-vpos:paragraph; -aw-top-pos:0pt; -aw-wrap-type:inline" />∠BAC.
∠BAC=∠BDC,即∠BDC=img src="http://thumb.zyjl.cn/questionBank/Upload/2017/12/28/23/3361039e/SYS201712282320308096520713_DA/SYS201712282320308096520713_DA.015.png" width="16" height="41" style="-aw-left-pos:0pt; -aw-rel-hpos:column; -aw-rel-vpos:paragraph; -aw-top-pos:0pt; -aw-wrap-type:inline" />∠BAC.
故⑤正确。
故答案为:①②④⑤。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AB=AC,E在BA的延长线上,AD平分∠CAE.
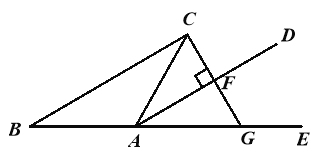
(1)求证:AD∥BC;
(2)过点C作CG⊥AD于点F,交AE于点G.若AF=4,求BC的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法中,正确的个数是( ) ①斜边和一直角边对应相等的两个直角三角形全等;
②有两边和它们的对应夹角相等的两个直角三角形全等;
③一锐角和斜边对应相等的两个直角三角形全等;
④两个锐角对应相等的两个直角三角形全等.
A.1个
B.2个
C.3个
D.4个 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知三角形的两边及其夹角,求作这个三角形时,第一步骤应为( )
A. 作一条线段等于已知线段
B. 作一个角等于已知角
C. 作两条线段等于已知三角形的边,并使其夹角等于已知角
D. 先作一条线段等于已知线段或先作一个角等于已知角
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,∠A=36°,AB=AC,BD平分∠ABC,DE∥BC,则图中等腰三角形的个数( ).
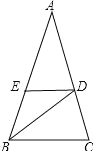
A.1个 B.3个 C.4个 D.5个
-
科目: 来源: 题型:
查看答案和解析>>【题目】三棱柱有5个面、6个顶点、9条棱,四棱柱有6个面、8个顶点、12条棱,五棱柱有7个面、10个顶点、15条棱,……由此可推测n棱柱有____个面、____ 个顶点、____条棱
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列图形中,既是轴对称图形,又是中心对称图形的是( )
A. 角B. 等边三角形C. 平行四边形D. 矩形
相关试题

