【题目】如图,平面直角坐标系中,矩形OABC的边与函数y=![]() (x>0)图象交于E,F两点,且F是BC的中点,则四边形ACFE的面积等于( )
(x>0)图象交于E,F两点,且F是BC的中点,则四边形ACFE的面积等于( )
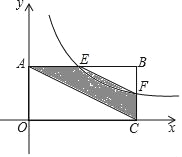
A. 4 B. 6 C. 8 D. 不能确定
参考答案:
【答案】B
【解析】
由四边形OABC是矩形,F是BC的中点,可设F(m,n),则B(m,2n),又E点在抛物线上,则E(![]() ,2n).可以用含m,n的式子表示出矩形OABC,三角形AOC和三角形BEF的面积.F在反比例函数的图形上可得到mn的关系,
,2n).可以用含m,n的式子表示出矩形OABC,三角形AOC和三角形BEF的面积.F在反比例函数的图形上可得到mn的关系,
再依据S四边形ACFE =S矩形OABC-S△AOC-S△BEF.即可求.
解:∵边形OABC是矩形,F是BC的中点,
∴可设F(m,n),则B(m,2n),又E点在抛物线上,则E(![]() ,2n),
,2n),
∵F在抛物线上,
∴mn=8,
∵F(m,n),B(m,2n), E(![]() ,2n),
,2n),
∴OA=2n,AB=OC=m,AE=![]() ,BF=n,
,BF=n,
∴S矩形OABC=2mn,
S△AOC =![]() ×OA×OC==
×OA×OC==![]() ×2n×m=mn,
×2n×m=mn,
S△BEF =![]() ×BE×BF=
×BE×BF=![]() ×(m-
×(m-![]() )×n=
)×n=![]() mn-4,
mn-4,
∵S四边形ACFE =S矩形OABC-S△AOC-S△BEF,
∴S四边形ACFE =2mn-mn-(![]() mn-4)=
mn-4)=![]() mn+2,
mn+2,
∵mn=8,
∴S四边形ACFE =![]() mn+2=6.
mn+2=6.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知A是双曲线y=
 在第一象限上的一动点,连接AO并延长交另一分支于点B,以AB为边作等边三角形ABC,点C在第四象限,已知点C的位置始终在一函数图象上运动,则这个函数解析式为( )
在第一象限上的一动点,连接AO并延长交另一分支于点B,以AB为边作等边三角形ABC,点C在第四象限,已知点C的位置始终在一函数图象上运动,则这个函数解析式为( )
A. y=﹣
 B. y=﹣
B. y=﹣ (x>0) C. y=﹣6x(x>0) D. y=6x(x>0)
(x>0) C. y=﹣6x(x>0) D. y=6x(x>0) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,两个边长分别为a,b(a>b)的正方形连在一起,三点C,B,F在同一直线上,反比例函数y=
 在第一象限的图象经过小正方形右下顶点E.若OB2﹣BE2=8,则k的值是( )
在第一象限的图象经过小正方形右下顶点E.若OB2﹣BE2=8,则k的值是( )
A. 3 B. 4 C. 5 D. 4

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,菱形ABCO的顶点O为坐标原点,边CO在x轴正半轴上,∠AOC=60°,反比例函数y=
 (x>0)的图象经过点A,交菱形对角线BO于点D,DE⊥x轴于点E,则CE长为( )
(x>0)的图象经过点A,交菱形对角线BO于点D,DE⊥x轴于点E,则CE长为( )
A. 1 B.
 C. 2
C. 2 ﹣
﹣ D.
D.  ﹣1
﹣1 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形OABC的顶点A,C分别在x轴,y轴上,顶点B在第一象限,AB=1.将线段OA绕点O按逆时针方向旋转60°得到线段OP,连接AP,反比例函数
 (k≠0)的图象经过P,B两点,则k的值为______________.
(k≠0)的图象经过P,B两点,则k的值为______________.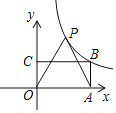
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=CB,∠ABC=90°,D为AB延长线上一点,点E在BC边上,且BE=BD,连结AE、DE、DC

①求证:△ABE≌△CBD;
②若∠CAE=30°,求∠BDC的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC是等边三角形,D为BC边上一个动点(D与B、C均不重合),AD=AE,∠DAE=60°,连接CE.
(1)求证:△ABD≌△ACE;
(2)求证:CE平分∠ACF;
(3)若AB=2,当四边形ADCE的周长取最小值时,求BD的长.

相关试题

