【题目】如图,两个边长分别为a,b(a>b)的正方形连在一起,三点C,B,F在同一直线上,反比例函数y=![]() 在第一象限的图象经过小正方形右下顶点E.若OB2﹣BE2=8,则k的值是( )
在第一象限的图象经过小正方形右下顶点E.若OB2﹣BE2=8,则k的值是( )

A. 3 B. 4 C. 5 D. 4![]()
参考答案:
【答案】B
【解析】
可设E点坐标为(m,n),由四边形OABC与四边形BDEF均为正方形,于是△ABO与△BDE均为等腰直角三角形,结合勾股定理可以表示出OB2与BE2,在结合OB2﹣BE2=8,可得到mn的乘积,即可求出k的值.
解:设E点坐标为(m,n),则AO+DE=m,AB-BD=n,
∵△ABO和△BED都是等腰直角三角形,
∴EB=![]() BD,OB=
BD,OB=![]() AB,BD=DE,OA=AB,
AB,BD=DE,OA=AB,
∵OB2-EB2=8,
∴2AB2-2BD2=8,
即AB2-BD2=4,
∴(AB+BD)(AB-BD)=4,
∴(AO+DE)(AB-BD)=4,
∴mn=4,
∴k=4.
故选:B.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某学校2019学年举行席地绘画大赛.共收到绘画作品480件,其中的优秀作品评出了一、二、三等奖.
占获奖总数的几分之几
获奖作品的件数
一等奖

b
二等奖
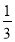
c
三等奖
a
96
(1)则a= ;b= ;c= ;
(2)学校决定为获一等奖同学每人购买一个书包,获得二等奖同学每人购买一个文具盒,获得三等奖同学每人购买一支钢笔,并且每位获奖同学颁发一个证书,已知文具盒单价是书包单价的
 ,证书的单价是文具盒单价的
,证书的单价是文具盒单价的 ,钢笔的单介是文具盒单价的
,钢笔的单介是文具盒单价的 ,学校购买书包、文具盒、钢笔共用4000元,那么学校购买证书共用了多少元?
,学校购买书包、文具盒、钢笔共用4000元,那么学校购买证书共用了多少元? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC内接于⊙O,∠B=60°,CD是⊙O的直径,点P是CD延长线上的一点,且AP=AC.

(1)求证:PA是⊙O的切线;
(2)若PD=
 ,求⊙O的直径.
,求⊙O的直径. -
科目: 来源: 题型:
查看答案和解析>>【题目】一辆货车从超市出发,向东走了2
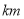 到达小刚家,继续向东走了3
到达小刚家,继续向东走了3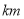 到达小红家,又向西走了9
到达小红家,又向西走了9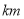 到达小英家,最后回到超市.
到达小英家,最后回到超市.(1)请以超市为原点,以向东方向为正方向,用1个单位长度表示1
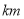 ,画出数轴,在数轴上表示出小刚家、小红家、小英家的位置;
,画出数轴,在数轴上表示出小刚家、小红家、小英家的位置;(2)小英家距小刚家有多远?
(3)货车一共行驶了多少千米?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=ax2+bx+c的图象经过点A(﹣2,0),点B(4,0),点D(2,4),与y轴交于点C,作直线BC,连接AC,CD.

(1)求抛物线的函数表达式;
(2)E是抛物线上的点,求满足∠ECD=∠ACO的点E的坐标;
(3)点M在y轴上且位于点C上方,点N在直线BC上,点P为第一象限内抛物线上一点,若以点C,M,N,P为顶点的四边形是菱形,求菱形的边长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知在纸面上有一数轴(如图),折叠纸面.
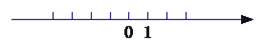
(1)若1表示的点与-1表示的点重合,则-2表示的点与数 表示的点重合;
(2)若-1表示的点与3表示的点重合,回答以下问题:
① 5表示的点与数 表示的点重合;
② 若数轴上A、B两点之间的距离为9(A在B的左侧),且A、B两点经折叠后重合,求A、B两点表示的数是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知反比例函数y1=
 的图象与一次函数y2=ax+b的图象交于点A(1,4)和点B(m,-2).
的图象与一次函数y2=ax+b的图象交于点A(1,4)和点B(m,-2).(1)求这两个函数的表达式;
(2)根据图象直接写出一次函数的值大于反比例函数的值的x的取值范围.

相关试题

