【题目】如图,已知反比例函数y=kx-1(k>0)的图象与一次函数图象y=﹣x+4交于a、b两点,点a的纵坐标为3.
(1)求反比例函数的解析;
(2)y轴上是否存在一点P,使2∠APB=∠AOB?若存在,求出点P的坐标;若不存在,请说明理由.

参考答案:
【答案】(0, ![]() )或(0,-
)或(0,-![]() )
)
【解析】(1)根据A在y=-x+4上,且点A的纵坐标为3,于是得到A(3,1),由于点A在反比例函数![]() 的图象上,即可得到结论;(2)根据勾股定理得到OA=
的图象上,即可得到结论;(2)根据勾股定理得到OA=![]() ,根据2∠APB=∠AOB,于是推出点P在以O为圆心,以OA为半径的圆上,得到OP=
,根据2∠APB=∠AOB,于是推出点P在以O为圆心,以OA为半径的圆上,得到OP=![]() ,即可得到结论.
,即可得到结论.
解:(1)∵A在y=-x+4上,且点A的纵坐标为3,得到A(3,1),
∵点A在反比例函数![]() 的图象上,得k=3,
的图象上,得k=3,
∴反比例函数的解析为: ![]() .
.
(2)如图所示,
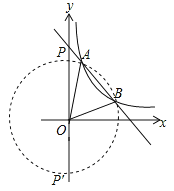
∵A(3,1),∴OA=![]() ,
,
∵2∠APB=∠AOB,
∴点P在以O为圆心,以OA为半径的圆上,
∴OP=![]() ,
,
∵点P在y轴上,
∴P(0, ![]() )或P
)或P![]() (0,
(0, ![]() ).
).
“点睛”本题考查反比例函数的图象与一次函数的交点问题,圆周角定理,勾股定理,正确作出辅助圆是解题关键.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AB=8,AC=6,AD、AE分别是其角平分线和中线,过点C作CG⊥AD于F,交AB于G,连接EF,求线段EF的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y1=kx+2与x轴交于点A(m,0)(m>4),与y轴交于点B,抛物线y2=ax2﹣4ax+c(a<0)经过A,B两点.P为线段AB上一点,过点P作PQ∥y轴交抛物线于点Q.
(1)当m=5时,
①求抛物线的关系式;
②设点P的横坐标为x,用含x的代数式表示PQ的长,并求当x为何值时,PQ=
 ;
;(2)若PQ长的最大值为16,试讨论关于x的一元二次方程ax2﹣4ax﹣kx=h的解的个数与h的取值范围的关系.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,二次函数y=ax2+bx+c的图象与x轴交于A、B两点,其中A点坐标为(-1,0),点C(0,5),另抛物线经过点(1,8),M为它的顶点.
(1)求抛物线的解析式;
(2)求出对称轴和顶点坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,写出△ABC各顶点的坐标以及△ABC关于x对称的△A1B1C1的各顶点坐标,并画出△ABC关于y对称的△A2B2C2.并求△ABC的面积。

-
科目: 来源: 题型:
查看答案和解析>>【题目】因式分解:m2﹣4mn+4n2= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法中,正确的是( )
A. 16的算术平方根是﹣4B. 25的平方根是5
C. ﹣27的立方根是﹣3D. 1的立方根是±1
相关试题

