【题目】二次函数y=ax2+bx+c(a≠0)的图象如图所示,根据图象解答下列问题.
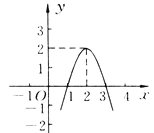
(1)写出方程ax2+bx+c=0的两个根;
(2)写出不等式ax2+bx+c>0的解集;
(3)写出y随x的增大而减小的自变量x的取值范围;
(4)若方程ax2+bx+c=k有两个不相等的实数根,求k的取值范围.
参考答案:
【答案】(1)x=1或x=3是方程ax2+bx+c=0的两个根;(2)l<x<3;(3)当x>2时,y随x的增大而减小;(4)k<2.
【解析】试题分析:(1)观察图形可以看出抛物线与x轴交于(1,0)和(3,0),即可解题
(2)根据抛物线y=ax2+bx+c,求得y>0的x取值范围即可解题;
(3)图中可以看出抛物线对称轴,即可解题;
(3)易求得抛物线解析式,根据方程△>0即可解题.
试题解析:(1)图中可以看出抛物线与x轴交于(1,0)和(3,0),
∴方程ax2+bx+c=0的两个根为x=1或x=3;
(2)不等式ax2+bx+c>0时,通过图中可以看出:当1<x<3时,y的值>0,
∴不等式ax2+bx+c>0的解集为(1,3);
(3)图中可以看出对称轴为x=2,
∴当x>2时,y随x的增大而减小;
(4)∵抛物线y=ax2+bx+c经过(1,0),(2,2),(3,0),
∴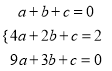 ,
,
解得:a=2,b=8,c=6,
∴2x2+8x6=k,移项得2x2+8x6k=0,
△=644(2)(6k)>0,
整理得:168k>0,
∴k<2时,方程ax2+bx+c=k有2个相等的实数根。
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的方程x2+(2m+1)x+m2+2=0有两个不相等的实数根,试判断直线y=(2m-3)x-4m+7能否经过点A(-2,4),并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在以O为原点的直角坐标系中,矩形OABC的两边OC、OA分别在x轴、y轴的正半轴上,反比例函数
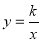 (x>0)与AB相交于点D,与BC相交于点E,若BD=3AD,且△ODE的面积是9,则k的值是( )
(x>0)与AB相交于点D,与BC相交于点E,若BD=3AD,且△ODE的面积是9,则k的值是( )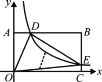
A.
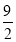 B.
B.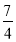 C.
C.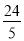 D.12
D.12 -
科目: 来源: 题型:
查看答案和解析>>【题目】两个反比例函数
 和
和 在第一象限内的图象如图所示,点P在
在第一象限内的图象如图所示,点P在 的图象上,PC⊥
的图象上,PC⊥ 轴于点C,交
轴于点C,交 的图象于点A,PC⊥
的图象于点A,PC⊥ 轴于点D,交
轴于点D,交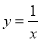 的图象于点B. 当点P在
的图象于点B. 当点P在 的图象上运动时,以下结论:
的图象上运动时,以下结论:①

②
 的值不会发生变化
的值不会发生变化③PA与PB始终相等
④当点A是PC的中点时,点B一定是PD的中点.
其中一定不正确的是( )

A. ① B. ② C. ③ D. ④
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)-42×
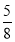 -(-5)×0.25×(-4)3
-(-5)×0.25×(-4)3(2)(4
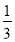 -3
-3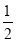 )×(-2)-2
)×(-2)-2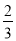 ÷(-
÷(-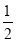 )
)(3)(-
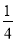 )2÷(-
)2÷(-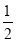 )4×(-1)4 -(1
)4×(-1)4 -(1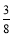 +1
+1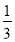 -2
-2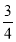 )×24
)×24(4)(
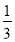 -
- )×52÷|-
)×52÷|-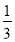 |+(-
|+(- )0+(0.25)2019×42019
)0+(0.25)2019×42019 -
科目: 来源: 题型:
查看答案和解析>>【题目】把棱长为1cm的若干个小正方体摆放如图所示的几何体,然后在露出的表面上涂上颜色
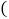 不含底面
不含底面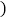
 该几何体中有多少小正方体?
该几何体中有多少小正方体? 画出主视图.
画出主视图.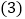 求出涂上颜色部分的总面积.
求出涂上颜色部分的总面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,已知抛物线P:y=ax2+bx+c(a≠0)与x轴交于A,B两点(点A在x轴的正半轴上),与y轴交于点C,矩形DEFG的一条边DE在线段AB上,顶点F,G分别在线段BC,AC上,抛物线P上的部分点的横坐标对应的纵坐标如下.

(1)求A,B,C三点的坐标;
(2)若点D的坐标为(m,0),矩形DEFG的面积为S,求S与m的函数关系式,并指出m的取值范围;
(3)当矩形DEFG的面积S最大时,连接DF并延长至点M,使FM=k·DF,若点M不在抛物线P上,求k的取值范围;
(4)若点D的坐标为(1,0),求矩形DEFG的面积.
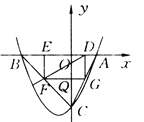
相关试题

