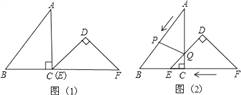
【题目】已知:把Rt△ABC和Rt△DEF按如图(1)摆放(点C与点E重合),点B、C(E)、F在同一条直线上,∠ACB=∠EDF=90°,∠DEF=45°,AC=8cm,BC=6cm,EF=9cm.如图(2),△DEF从图(1)的位置出发,以1cm/s的速度沿CB向△ABC匀速移动,在△DEF移动的同时,点P从△ABC的顶点B出发,以2cm/s的速度沿BA匀速移动,当△DEF的顶点D移动到AC边上时,△DEF停止移动,点P也随之停止移动,DE与AC相交于点Q,连接PQ,设移动时间为t(s)(0<t<4.5).
解答下列问题:
(1)当t为何值时,点A在线段PQ的垂直平分线上?
(2)连接PE,设四边形APEC的面积为y(cm2),求y与t之间的函数关系式,是否存在某一时刻t,使面积y最小?若存在,求出y的最小值;若不存在,说明理由;
(3)是否存在某一时刻t,使P、Q、F三点在同一条直线上?若存在,求出此时t的值;若不存在,说明理由.
参考答案:
【答案】(1)2s;(2)存在,![]() cm2;(3)存在,t=1s
cm2;(3)存在,t=1s
【解析】试题分析:
(1)由已知条件先证△ECQ中,CQ=EC=t,由此可得AQ=8-t,由勾股定理可得AB=10,由此可得AP=AB-BP=10-2t,若点A在PQ的垂直平分线上,则有AP=AQ,由此可得关于t的方程,解此方程即可得到所求的t的值;
(2)如图1,过点P作PM⊥BE,交BE于M,由sinB=![]() =
=![]() ,可得
,可得![]() ,由此可得PM=
,由此可得PM=![]() ,再由S四边形APEC=S△ABC-S△APE即可用含t的式子表达出四边形APEC的面积了,再将所得表达式配方,即可求得当t为何值时,四边形ABEC的面积最小了;
,再由S四边形APEC=S△ABC-S△APE即可用含t的式子表达出四边形APEC的面积了,再将所得表达式配方,即可求得当t为何值时,四边形ABEC的面积最小了;
(3)如图2,假设在某一时刻,点P、F、Q在同一直线上,此时,过点P作PN⊥AC于点N,则易得△PAN∽△BAC,由此可得![]() ,即
,即![]() ,则可得PN=6﹣
,则可得PN=6﹣![]() t ,AN=8﹣
t ,AN=8﹣![]() t,这样即可得到NQ=8﹣t﹣(8﹣
t,这样即可得到NQ=8﹣t﹣(8﹣![]() )=
)=![]() ,再证△QCF∽△QNP从而可得
,再证△QCF∽△QNP从而可得![]() ,即
,即![]() ,由此即可解得所求的t的值了.
,由此即可解得所求的t的值了.
试题解析:
(1)∵点A在线段PQ的垂直平分线上,
∴AP=AQ;
∵∠DEF=45°,∠ACB=90°,∠DEF+∠ACB+∠EQC=180°,
∴∠EQC=45°;
∴∠DEF=∠EQC;
∴CE=CQ;
由题意知:CE=t,BP=2t,
∴CQ=t;
∴AQ=8﹣t;
在Rt△ABC中,由勾股定理得:AB=10cm;
则AP=10﹣2t;
∴10﹣2t=8﹣t;
解得:t=2;
答:当t=2s时,点A在线段PQ的垂直平分线上;
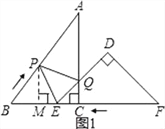
(2)如下图1,过P作PM⊥BE,交BE于M,
∴∠BMP=90°;
在Rt△ABC和Rt△BPM中,sinB=![]() =
=![]() ,
,
∴![]() ,
,
∴PM=![]() ,
,
∵BC=6cm,CE=t,
∴BE=6﹣t,
∴y=S△ABC﹣S△BPE
=![]() BCAC﹣
BCAC﹣![]() BEPM
BEPM
=![]() ×6×8﹣
×6×8﹣![]() (6﹣t)×
(6﹣t)×![]()
=![]()
=![]() ,
,
∵![]() ,
,
∴抛物线开口向上;
∴当t=3时,y最小=![]() ;
;
答:当t=3s时,四边形APEC的面积最小,最小面积为![]() cm2.
cm2.
(3)假设存在某一时刻t,使点P、Q、F三点在同一条直线上;
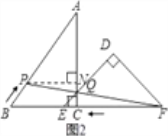
如图2,过P作PN⊥AC,交AC于N
∴∠ANP=∠ACB=∠PNQ=90°;
∵∠PAN=∠BAC,
∴△PAN∽△BAC,
∴![]() ,
,
∴![]() ,
,
∴PN=6﹣![]() t ,AN=8﹣
t ,AN=8﹣![]() t,
t,
∵NQ=AQ﹣AN,
∴NQ=8﹣t﹣(8﹣![]() )=
)=![]() ,
,
∵∠ACB=90°,B、C、E、F在同一条直线上,
∴∠QCF=90°,∠QCF=∠PNQ;
∵∠FQC=∠PQN,
∴△QCF∽△QNP;
∴![]() ,即
,即![]() ;
;
∵0<t<4.5,
∴![]() ,
,
解得:t=1;
答:当t=1s,点P、Q、F三点在同一条直线上.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,A(4,0),B(1,3),以OA、OB为边作平行四边形OACB,反比例函数y=
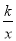 的图象经过点C.
的图象经过点C.
(1)求k的值;
(2)根据图象,直接写出y<3时自变量x的取值范围;
(3)将平行四边形OACB向上平移几个单位长度,使点B落在反比例函数的图象上.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
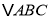 中,点D,E分别在边AC,AB上,BD与CE交于点O,给出下列三个条件:①∠EBO=∠DCO;②
中,点D,E分别在边AC,AB上,BD与CE交于点O,给出下列三个条件:①∠EBO=∠DCO;②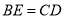 ;③
;③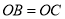 .
.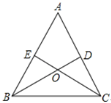
(1)上述三个条件中,由哪两个条件可以判定
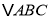 是等腰三角形?(用序号写出所有成立的情形)
是等腰三角形?(用序号写出所有成立的情形)(2)请选择(1)中的一种情形,说明你的理由.
-
科目: 来源: 题型:
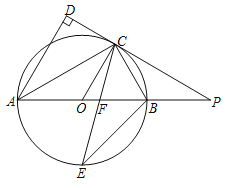
查看答案和解析>>【题目】如图,
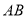 是⊙
是⊙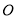 的直径,点
的直径,点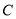 是⊙
是⊙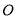 上一点,
上一点, 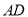 与过点
与过点 的切线垂直,垂足为点
的切线垂直,垂足为点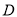 ,直线
,直线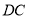 与
与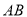 的延长线相交于点
的延长线相交于点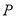 ,弦
,弦 平分∠
平分∠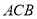 ,交
,交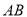 于点
于点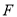 ,连接
,连接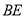 .
.
(1)求证:
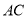 平分∠
平分∠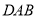 ;
;(2)求证:PC=PF;
(3)若
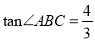 ,AB=14,求线段
,AB=14,求线段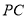 的长.
的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】一个不透明的袋子中,装有2个红球,1个白球,1个黄球,这些球除颜色外都相同.求下列事件的概率:
(1)搅匀后从中任意摸出1个球,恰好是红球;
(2)搅匀后从中任意摸出2个球,2个都是红球.
-
科目: 来源: 题型:
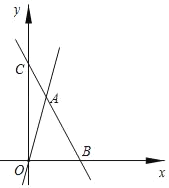
查看答案和解析>>【题目】已知:一个正比例函数与一个一次函数的图象交于点A(1,4)且一次函数的图象与x轴交于点B(3,0),坐标原点为O.
(1)求正比例函数与一次函数的解析式;
(2)若一次函数交与y轴于点C,求△ACO的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司在某市五个区投放共享单车供市民使用,投放量的分布及投放后的使用情况统计如下.
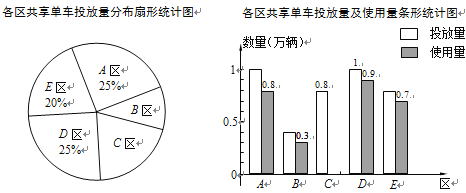
(1)该公司在全市一共投放了 万辆共享单车;
(2)在扇形统计图中,B区所对应扇形的圆心角为 °;
(3)该公司在全市投放的共享单车的使用量占投放量的85%,请计算C区共享单车的使用量并补全条形统计图.
相关试题

