【题目】如图,在![]() 中,点D,E分别在边AC,AB上,BD与CE交于点O,给出下列三个条件:①∠EBO=∠DCO;②
中,点D,E分别在边AC,AB上,BD与CE交于点O,给出下列三个条件:①∠EBO=∠DCO;②![]() ;③
;③![]() .
.
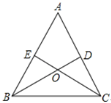
(1)上述三个条件中,由哪两个条件可以判定![]() 是等腰三角形?(用序号写出所有成立的情形)
是等腰三角形?(用序号写出所有成立的情形)
(2)请选择(1)中的一种情形,说明你的理由.
参考答案:
【答案】(1)①②或①③;(2)见解析.
【解析】
(1)由①②;①③.两个条件可以判定△ABC是等腰三角形,
(2)先求出∠ABC=∠ACB,即可证明△ABC是等腰三角形.
解:(1)①②;①③.
(2)选①③证明如下,
∵OB=OC,
∴∠OBC=∠OCB,
∵∠EBO=∠DCO,
又∵∠ABC=∠EBO+∠OBC,∠ACB=∠DCO+∠OCB,
∴∠ABC=∠ACB,
∴△ABC是等腰三角形.
选①②证明如下,
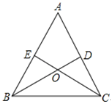
在△EBO与△DCO中,
∵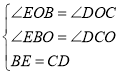 ,
,
∴△EBO≌△DCO(AAS),
∴OB=OC,
∴∠OBC=∠OCB,
∵∠EBO=∠DCO,
又∵∠ABC=∠EBO+∠OBC,∠ACB=∠DCO+∠OCB,
∴∠ABC=∠ACB,
∴AB=AC,
∴△ABC是等腰三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市出租车计费方式如图所示,请根据图象回答问题.
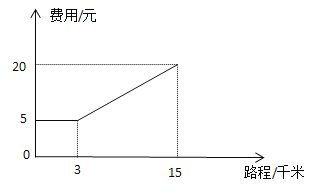
(1)出租车起价是多少元?在多少千米之内只收起价费?
(2)由图象求出起价里程走完之后每行驶1千米所增加的费用;
(3)小张想用30元坐车在该市游玩,试求他最多能走多少千米.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,小丽准备测一根旗杆AB的高度,已知小丽的眼睛离地面的距离EC=1.5米,第一次测量点C和第二次测量点D之间的距离CD=10米,∠AEG=30°,∠AFG=60°,请你帮小丽计算出这根旗杆的高度.(结果保留根号)
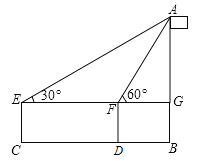
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,A(4,0),B(1,3),以OA、OB为边作平行四边形OACB,反比例函数y=
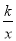 的图象经过点C.
的图象经过点C.
(1)求k的值;
(2)根据图象,直接写出y<3时自变量x的取值范围;
(3)将平行四边形OACB向上平移几个单位长度,使点B落在反比例函数的图象上.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 是⊙
是⊙ 的直径,点
的直径,点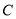 是⊙
是⊙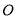 上一点,
上一点, 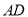 与过点
与过点 的切线垂直,垂足为点
的切线垂直,垂足为点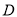 ,直线
,直线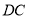 与
与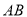 的延长线相交于点
的延长线相交于点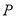 ,弦
,弦 平分∠
平分∠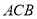 ,交
,交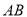 于点
于点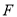 ,连接
,连接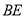 .
.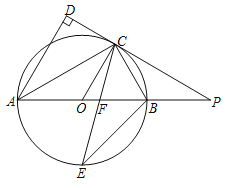
(1)求证:
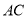 平分∠
平分∠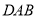 ;
;(2)求证:PC=PF;
(3)若
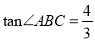 ,AB=14,求线段
,AB=14,求线段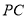 的长.
的长. -
科目: 来源: 题型:
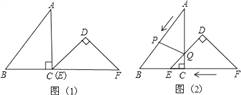
查看答案和解析>>【题目】已知:把Rt△ABC和Rt△DEF按如图(1)摆放(点C与点E重合),点B、C(E)、F在同一条直线上,∠ACB=∠EDF=90°,∠DEF=45°,AC=8cm,BC=6cm,EF=9cm.如图(2),△DEF从图(1)的位置出发,以1cm/s的速度沿CB向△ABC匀速移动,在△DEF移动的同时,点P从△ABC的顶点B出发,以2cm/s的速度沿BA匀速移动,当△DEF的顶点D移动到AC边上时,△DEF停止移动,点P也随之停止移动,DE与AC相交于点Q,连接PQ,设移动时间为t(s)(0<t<4.5).
解答下列问题:
(1)当t为何值时,点A在线段PQ的垂直平分线上?
(2)连接PE,设四边形APEC的面积为y(cm2),求y与t之间的函数关系式,是否存在某一时刻t,使面积y最小?若存在,求出y的最小值;若不存在,说明理由;
(3)是否存在某一时刻t,使P、Q、F三点在同一条直线上?若存在,求出此时t的值;若不存在,说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个不透明的袋子中,装有2个红球,1个白球,1个黄球,这些球除颜色外都相同.求下列事件的概率:
(1)搅匀后从中任意摸出1个球,恰好是红球;
(2)搅匀后从中任意摸出2个球,2个都是红球.
相关试题

