【题目】如图,在平面直角坐标系中,⊙P与x轴相切,与y轴相交于A(0,2),B(0,8),则圆心P的坐标是( ) 
A.(5,3)
B.(5,4)
C.(3,5)
D.(4,5)
参考答案:
【答案】D
【解析】解: 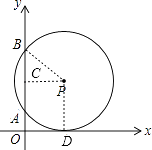
如图,过P作PC⊥AB于点C,过P作PD⊥x轴于点D,连接PB,
∵P为圆心,
∴AC=BC,
∵A(0,2),B(0,8),
∴AB=8﹣2=6,
∴AC=BC=3,
∴OC=8﹣3=5,
∵⊙P与x轴相切,
∴PD=PB=OC=5,
在Rt△PBC中,由勾股定理可得PC= ![]() =
= ![]() =4,
=4,
∴P点坐标为(4,5),
故选D.
过P作PC⊥AB于点C,过P作PD⊥x轴于点D,由切线的性质可求得PD的长,则可得PB的长,由垂径定理可求得CB的长,在Rt△PBC中,由勾股定理可求得PC的长,从而可求得P点坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】把下面的说理过程补充完整:
已知:如图,∠1+∠2=180°,∠3=∠B,试判断∠AED与∠C的关系,并说明理由.

解:∠AED=∠C.
理由:∵∠1+∠ADG=180°(平角定义),∠1+∠2=180°(已知).
∴∠2=∠ADG.(_____________)
∴EF∥AB(______________).
∴∠3=∠AED(_____________).
∵∠3=∠B(已知),
∴∠B=________(________________)
∴DE∥BC(__________________).
∴∠AED=∠C(_________________).
-
科目: 来源: 题型:
查看答案和解析>>【题目】一只蚂蚁在一个半圆形的花坛的周边寻找食物,如图1,蚂蚁从圆心O出发,按图中箭头所示的方向,依次爬完下列三条线路:(1)线段OA、(2)半圆弧AB、(3)线段BO后,回到出发点。已知蚂蚁在爬行过程中保持匀速,且在寻找到食物后停下来吃了2分钟。蚂蚁离出发点的距离s(蚂蚁所在位置与O点之间线段的长度)与时间t之间的图象如图2所示,问:
(1)花坛的半径是_______米,蚂蚁是在上述三条线路中的哪条上寻找到了食物_________(填(1)、(2)、或(3));
(2)蚂蚁的速度是_______米/分钟;

(3)蚂蚁从O点出发,直到回到O点,一共用时多少分钟?(
 )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】m、n互为相反数,x、y互为倒数,则2015m+2015n-2016xy=____________
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图的三角形纸片中,AB=AC,BC=12cm,∠C=30°,折叠这个三角形,使点B落在AC的中点D处,折痕为EF,那么BF的长为cm.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知AM∥CN,点B为平面内一点,AB⊥BC于B.
(1)如图1,直接写出∠A和∠C之间的数量关系________;
(2)如图2,过点B作BD⊥AM于点D,试说明:∠ABD=∠C;
(3)如图3,在(2)问的条件下,点E在DM上,且BE平分∠DBC,试说明∠ABE=∠AEB.

相关试题

