【题目】11世纪的一位阿拉伯数学家曾提出一个“鸟儿捉鱼”问题:小溪边长着两棵棕榈树,恰好隔岸相望一棵棕榈树高是30肘尺(肘尺是古代的长度单位),另外一棵高20肘尺;两棵棕榈树的树干间的距离是50肘尺.每棵树的树顶上都停着一只鸟.忽然,两只鸟同时看见棕榈树间的水面上游出一条鱼,它们立刻以相同的速度飞去抓鱼,并且同时到达目标.问:这条鱼出现的地方离比较高的棕榈树的树根有多远?
参考答案:
【答案】20.
【解析】
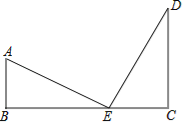
试题根据题意画出图形,利用勾股定理建立方程,求出x的值即可.
试题解析:画图解决,通过建模把距离转化为线段的长度.
由题意得:AB=20,DC=30,BC=50,设EC为x肘尺,BE为(50﹣x)肘尺,
在Rt△ABE和Rt△DEC中,![]() ,
,![]() ,
,
又∵AE=DE,∴![]() ,解得:
,解得:![]() ,
,
答:这条鱼出现的地方离比较高的棕榈树的树根20肘尺.
-
科目: 来源: 题型:
查看答案和解析>>【题目】作图题.
(1)如图,在图①所给的方格纸中,每个小正方形的边长都是1,标号为①②③的三个三角形均为格点三角形(顶点在方格的顶点处),请按要求将图②中的指定图形分割成三个三角形,使它们与标号为①②③的三个三角形分别对应全等(分割线画成实线);
(2)如图③,在边长为1个单位长度的小正方形组成的正方形网格中,点
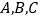 都在小正方形的顶点上.
都在小正方形的顶点上.①在图中画出与
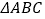 关于直线
关于直线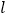 成轴对称的
成轴对称的 ;
;②请在直线
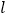 上找一点
上找一点 ,使得
,使得 的距离之和最小.
的距离之和最小.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列函数:①y=﹣x;②y=2x;③y=﹣
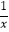 ;④y=x2(x<0),y随x的增大而减小的函数有( )
;④y=x2(x<0),y随x的增大而减小的函数有( )
A.1个
B.2个
C.3个
D.4个 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 中,
中,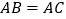 ,
, 是边
是边 的中点,以
的中点,以 为腰向外作等腰直角三角形
为腰向外作等腰直角三角形 ,
, ,连接
,连接 ,交
,交 于点
于点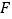 ,交
,交 于点
于点 ,连接
,连接 .
.(1)若
 ,则
,则 ;
;(2)求证:
 ;
;(3)若
 ,则
,则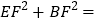 .
.
-
科目: 来源: 题型:
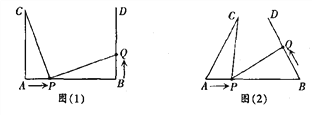
查看答案和解析>>【题目】如图(1),AB=4cm,AC⊥AB,BD⊥AB,AC=BD=3cm.点P在线段AB上以1cm/s的速度由点A向点B运动,同时,点Q在线段BD上由点B向点D运动.它们运动的时间为t(s).
(1)若点Q的运动速度与点P的运动速度相等,当t=1时,△ACP与△BPQ是否全等,请说明理由,并判断此时线段PC和线段PQ的位置关系;
(2)如图(2),将图(1)中的“AC⊥AB,BD⊥AB”为改“∠CAB=∠DBA=60°”,其他条件不变.设点Q的运动速度为x cm/s,是否存在实数x,使得△ACP与△BPQ全等?若存在,求出相应的x、t的值;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,二次函数y=ax2+bx+c的图象开口向上,对称轴为直线x=1,图象经过(3,0),下列结论中,正确的一项是( )
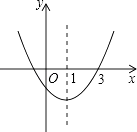
A.abc<0
B.4ac﹣b2<0
C.a﹣b+c<0
D.2a+b<0 -
科目: 来源: 题型:
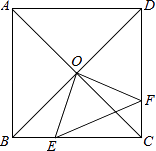
查看答案和解析>>【题目】如图,正方形ABCD中,AB=8cm,对角线AC,BD相交于点O,点E,F分别从B,C两点同时出发,以1cm/s的速度沿BC,CD运动,到点C,D时停止运动,设运动时间为t(s),△OEF的面积为s(cm2),则s(cm2)与t(s)的函数关系可用图象表示为( )
A.
B.
C.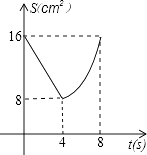
D.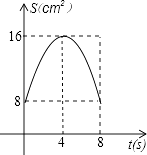
相关试题

