【题目】如图,已知点D在△ABC的BC边上,DE∥AC交AB于E,DF∥AB交AC于F.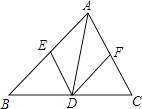
(1)求证:AE=DF;
(2)若AD平分∠BAC,试判断四边形AEDF的形状,并说明理由.
参考答案:
【答案】
(1)证明:∵DE∥AC,∠ADE=∠DAF,
同理∠DAE=∠FDA,
∵AD=DA,
∴△ADE≌△DAF,
∴AE=DF
(2)证明:若AD平分∠BAC,四边形AEDF是菱形,
∵DE∥AC,DF∥AB,
∴四边形AEDF是平行四边形,
∴∠DAF=∠FDA.
∴AF=DF.
∴平行四边形AEDF为菱形
【解析】(1)根据已知条件由角边角可证△ADE≌△DAF,则AE=DF;(2)由已知可证四边形AEDF是平行四边形,再由AF=DF可证平行四边形AEDF为菱形。
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校为了进一步改进本校七年级数学教学,提高学生学习数学的兴趣,校教务处在七年级所有班级中,每班随机抽取了6名学生,并对他们的数学学习情况进行了问卷调查.我们从所调查的题目中,特别把学生对数学学习喜欢程度的回答(喜欢程度分为:“A﹣非常喜欢”、“B﹣比较喜欢”、“C﹣不太喜欢”、“D﹣很不喜欢”,针对这个题目,问卷时要求每位被调查的学生必须从中选一项且只能选一项)结果进行了统计,现将统计结果绘制成如下两幅不完整的统计图.

请你根据以上提供的信息,解答下列问题:(1)补全上面的条形统计图和扇形统计图;
(2)所抽取学生对数学学习喜欢程度的众数是 ;
(3)若该校七年级共有960名学生,请你估算该年级学生中对数学学习“不太喜欢”的有多少人?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知直线l与⊙O相离,OA⊥l于点A,交⊙O于点P,OA=5,AB与⊙O相切于点B,BP的延长线交直线l于点C.
(1)求证:AB=AC;
(2)若
 ,求⊙O的半径.
,求⊙O的半径.
-
科目: 来源: 题型:
查看答案和解析>>【题目】今年参加我市初中毕业生学业考试的总人数约为56000人,这个数据用科学记数法表示为( )
A.5.6×103
B.5.6×104
C.5.6×105
D.0.56×105 -
科目: 来源: 题型:
查看答案和解析>>【题目】在矩形ABCD中,AB=6cm,BC=12cm,点P从点A出发,沿AB边向点B以每秒1cm的速度移动,同时,点Q从点B出发沿BC边向点C以每秒2cm的速度移动.如果P、Q两点在分别到达B、C两点后就停止移动,回答下列问题:
(1)运动开始后第几秒时,△PBQ的面积等于8cm2?
(2)当运动开始后
 秒时,试判断△DPQ的形状;
秒时,试判断△DPQ的形状;(3)在运动过程中,是否存在这样的时刻,使以Q为圆心,PQ为半径的圆正好经过点D?若存在,求出运动时间;若不存在,请说明理由.
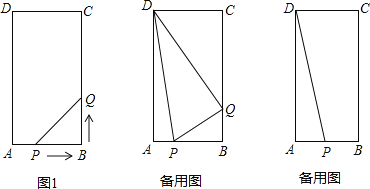
-
科目: 来源: 题型:
查看答案和解析>>【题目】某青年旅社有60间客房供游客居住,在旅游旺季,当客房的定价为每天200元时,所有客房都可以住满.客房定价每提高10元,就会有1个客房空闲,对有游客入住的客房,旅社还需要对每个房间支出20元/每天的维护费用,设每间客房的定价提高了x元.
(1)填表(不需化简)
入住的房间数量
房间价格
总维护费用
提价前
60
200
60×20
提价后
(2)若该青年旅社希望每天纯收入为14000元且能吸引更多的游客,则每间客房的定价应为多少元?(纯收入=总收入﹣维护费用)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC和△DCB中,AB=DC,AC=DB,AC与DB交于点M.
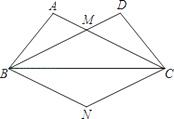
(1)求证:△ABC≌△DCB;
(2)过点C作CN∥BD,过点B作BN∥AC,CN与BN交于点N,试判断线段BN与CN的数量关系,并证明你的结论.
相关试题

