【题目】如图,△ABC中,AD是高,CE是中线,点G是CE的中点,DG⊥CE,点G为垂足. 
(1)求证:DC=BE;
(2)若∠AEC=66°,求∠BCE的度数.
参考答案:
【答案】
(1)证明:如图,
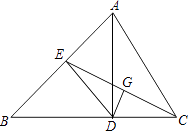
∵G是CE的中点,DG⊥CE,
∴DG是CE的垂直平分线,
∴DE=DC,
∵AD是高,CE是中线,
∴DE是Rt△ADB的斜边AB上的中线,
∴DE=BE= ![]() AB,
AB,
∴DC=BE;
(2)解:∵DE=DC,
∴∠DEC=∠BCE,
∴∠EDB=∠DEC+∠BCE=2∠BCE,
∵DE=BE,
∴∠B=∠EDB,
∴∠B=2∠BCE,
∴∠AEC=3∠BCE=66°,则∠BCE=22°.
【解析】(1)由G是CE的中点,DG⊥CE得到DG是CE的垂直平分线,根据线段垂直平分线的性质得到DE=DC,由DE是Rt△ADB的斜边AB上的中线,根据直角三角形斜边上的中线等于斜边的一半得到DE=BE= ![]() AB,即可得到DC=BE;(2)由DE=DC得到∠DEC=∠BCE,由DE=BE得到∠B=∠EDB,根据三角形外角性质得到∠EDB=∠DEC+∠BCE=2∠BCE,则∠B=2∠BCE,由此根据外角的性质来求∠BCE的度数.
AB,即可得到DC=BE;(2)由DE=DC得到∠DEC=∠BCE,由DE=BE得到∠B=∠EDB,根据三角形外角性质得到∠EDB=∠DEC+∠BCE=2∠BCE,则∠B=2∠BCE,由此根据外角的性质来求∠BCE的度数.
【考点精析】本题主要考查了直角三角形斜边上的中线的相关知识点,需要掌握直角三角形斜边上的中线等于斜边的一半才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABE中,∠A=105°,AE的垂直平分线MN交BE于点C,且AB+BC=BE,则∠B的度数是( )

A. 45° B. 60° C. 50° D. 55°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在△ABC中,AB=AC,BD,CE是角平分线,图中的等腰三角形共有( )

A. 6个 B. 5个 C. 4个 D. 3个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 ,
, ,AE平分
,AE平分 ,
, ,交AC延长线于F,且垂足为E,则下列结论:
,交AC延长线于F,且垂足为E,则下列结论: ;
; ;
; ,
, ;
; 其中正确的结论有______
其中正确的结论有______ 填写序号
填写序号

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知BD,CE是△ABC的两条高,直线BD,CE相交于点H.

(1)若∠BAC=100°,求∠DHE的度数;
(2)若△ABC中∠BAC=50°,直接写出∠DHE的度数是____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等边三角形ABC中,AD⊥BC于点D,以AD为一边向右作等边三角形ADE,DE与AC交于点F.
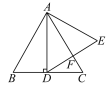
(1)试判断DF与EF的数量关系,并给出证明;
(2)若CF的长为2 cm,试求等边三角形ABC的边长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠ACB=90°,AC=BC,D为△ABC内一点,∠CAD=∠CBD=15°,E为AD延长线上的一点,且CE=AC.

(1)求∠CDE的度数;
(2)若点M在DE上,且DC=DM,求证:ME=BD.
相关试题

